媒介変数表示とは グラフの書き方と考え方


しかし同じことを言っても仕方ないので、私からは「媒介変数表示でなくても扱える図形」について話したいと思います。 異なる変数の間の陰伏的な関係を記述する媒介変数は、その媒介変数が変化したときの系の振る舞いを見るという意味で「変数」と見ることができるが、対照的に主変数の変化に伴う系の振る舞いを調べたい場合などでは、しばしば補助変数は(「値を取り換えることができる」という意味で値は任意にとれるけれども)「定数」として扱われる。


しかし同じことを言っても仕方ないので、私からは「媒介変数表示でなくても扱える図形」について話したいと思います。 異なる変数の間の陰伏的な関係を記述する媒介変数は、その媒介変数が変化したときの系の振る舞いを見るという意味で「変数」と見ることができるが、対照的に主変数の変化に伴う系の振る舞いを調べたい場合などでは、しばしば補助変数は(「値を取り換えることができる」という意味で値は任意にとれるけれども)「定数」として扱われる。
複数の大学・学部・学科・方式に合格している方は、複数の合格者数として集計。
一方、定点 に対して、 でないベクトル に平行な直線を考えます。


対称式については を見ると良いでしょう。 そこで、 媒介変数表示されたグラフの面積の検算方法について教えたいと思います! ガウスグリーンの定理が有効! 媒介変数表示されたグラフに囲まれた面積は、 ガウスグリーンの定理というものを用いると実は非常に簡単に計算できることが多いです。
7つまり、 xとyをtが媒介しているのです。
ちなみに、時計回りに動いているときには、マイナスをつければ面積になります。

どちらかお一人がお手続きをすれば、お二人分のプレゼントをお届けします。 言葉で言われても何が何やらなので、実際に図を書いてみます。 なお, x が独立変数であり、 y と z は x を変数とする関数である。
参考文献 [ ]. したがって、 閉じた曲線の内側の面積を求める検算のときにはガウスグリーンの定理によってパラメータの端から端まで積分し、もし負の値が求まってしまったらその絶対値を考えればよいことになります。
グラフの描き方には主に3通りある 媒介変数表示された曲線のグラフの描き方は 主に3通りあります。
つまり「軌跡」における媒介変数表示とは、経由することで解答まで辿り着くことのできる、いわば中継地点として活躍する文字のことをいいます。
動く直線と円の媒介変数表示 円の媒介変数表示の例として、直線を使うものも紹介します。
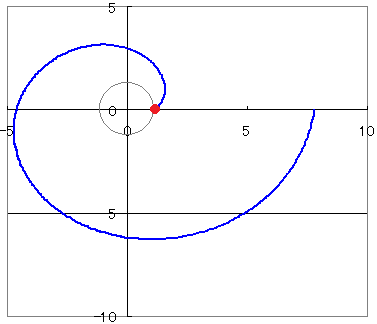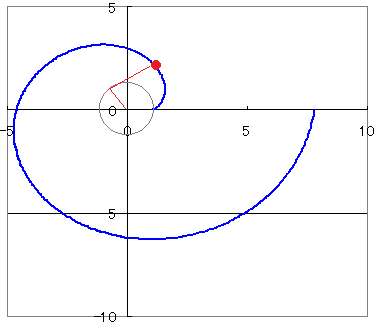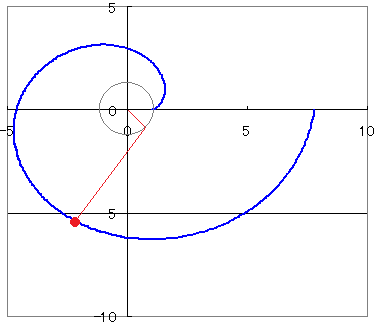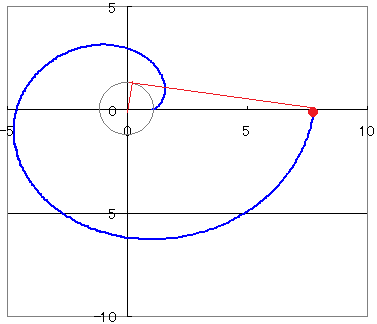
しかし現実問題、この式は高校数学においてはかなり扱い辛いです。 他にも空間上の点をtの媒介変数表示で表したり、結構便利です。 双曲線 双曲線に関しては少し違った見方で媒介変数表示を考えてみましょう。
14そのため、この表記も、単位円を表していると考えることができます。
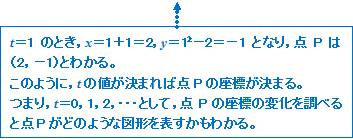
tの値がきまれば、点Pの座標であるx, yの値が決まりますね。
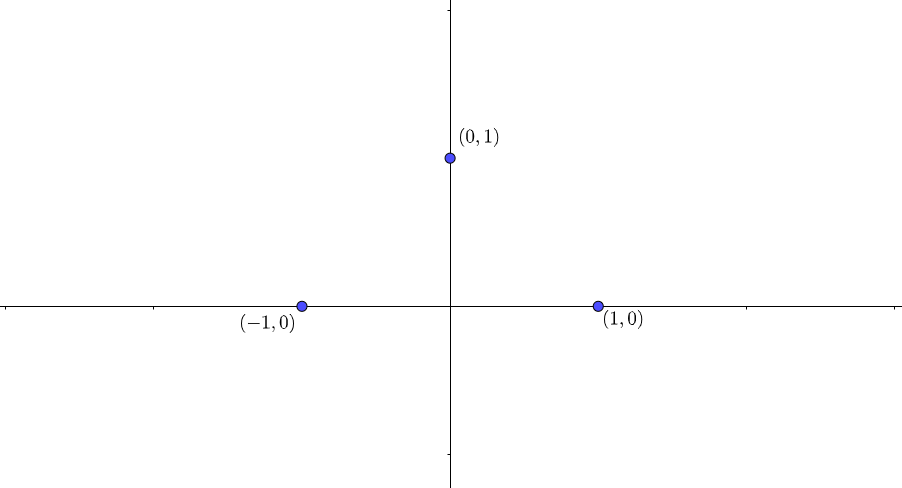

その他のいろいろな曲線 その他の大学入試で出題される曲線についての解説です。
入会フォームの「入会後に、ご紹介者の情報を登録する」にチェックを入れてください。
注 [ ] [] 注釈 [ ]• 大抵の文献では、単に開述語に引き渡される項という意味で変項と呼んで、代入の定義においてととを区別するという手段をとる。
つまり、 となる実数tが存在します。
2019. 入会完了 あなたと、あなたのお友だち・ごきょうだいに「教材」をお送りしますので、 プレゼント申し込み手続きを行う代表者を決め、0120-332211(9:00~21:00年末年始除く 通話料無料)までお電話ください。

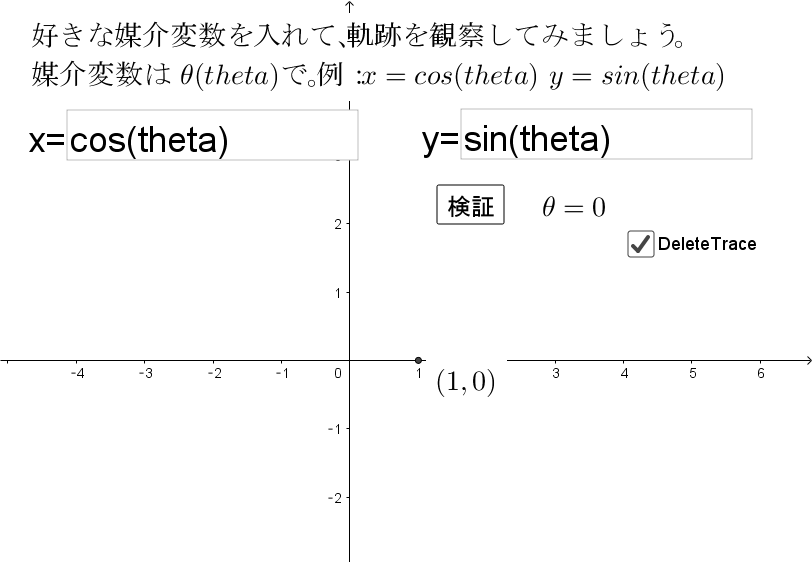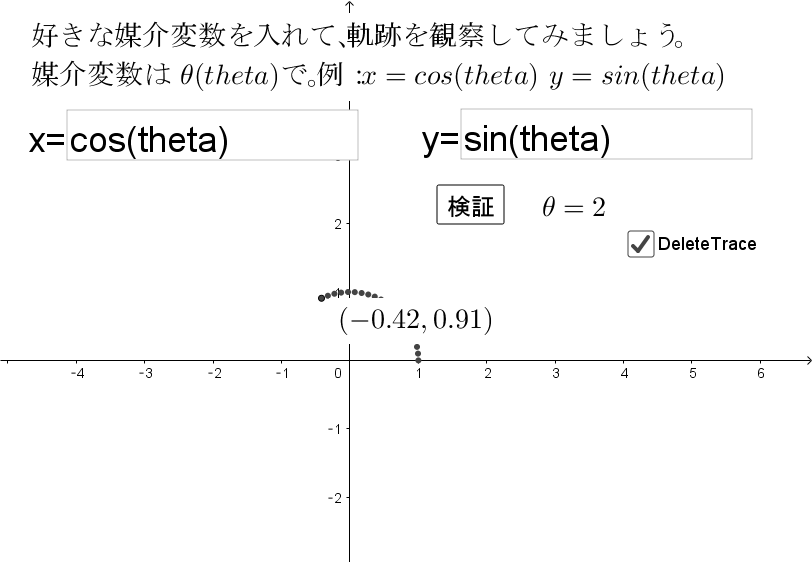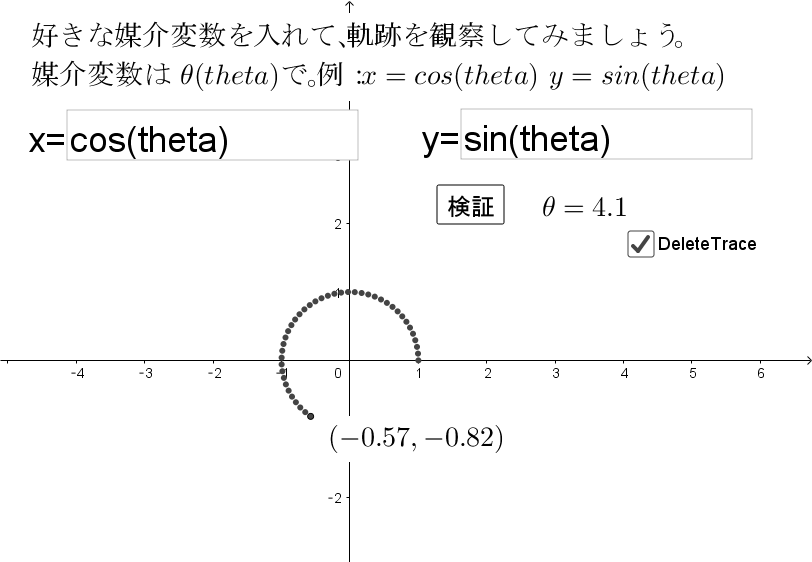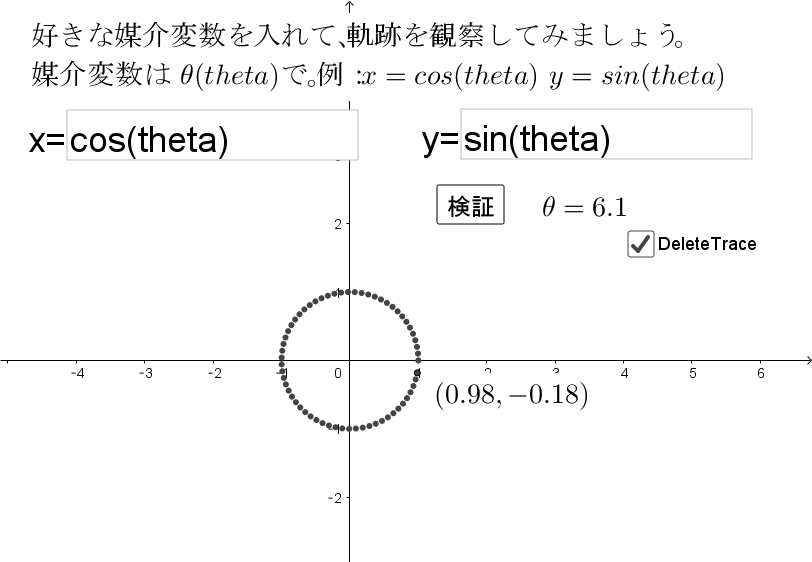
これが双曲線の媒介変数表示です。 お申し込みの際にご登録いただいたメールアドレスに、手続き完了のメールをお送りしますので、プレゼント申し込み手続きを行う代表者を決め、お手続きをお願いします。
17一般角を用いた円の媒介変数表示 と内容がかぶりますが、一般角を用いた円の媒介変数表示を見ていきましょう。
媒介変数表示されたグラフの描き方について詳しく説明した記事はこちら。
つまり、パラメータに伴って反時計まわりに動いてるグラフに囲まれた部分の面積なら、簡単に積分の式が立つよ、ということです。
これなら計算が進められそうです。