数学 的 帰納 法。 数学的帰納法のパターンまとめ

数学的帰納法

2つの命題を一気に数学的帰納法で示すという今回の解き方は上で紹介したどのパターンにも属さないので、なかなか議論のしかたが思いつきづらかったかと思います。 簡単にまとめておきます。 数列について漸化式ではなく、不等式のみが与えられています。

• 1日目が雨でした。

• 今まで解いてきた問題は前者ばかりでしたが、数列が絡んだ問題は大体後者になります。

数列(一般項から数学的帰納法まで)の要点

練習問題 次の等式が成り立つことを証明せよ。

7

• 数学的帰納法の基礎 帰納と演繹 数学的帰納法の「帰納」とは何かを説明します。

• 例えば、ファッションのトレンドは 「螺旋構造」になっているというのをご存知でしょうか？ 例えば、幅の広いワイドパンツは2年前だとダサい認定されたはずです。

【数列】数学的帰納法の意味と証明の具体例

これは、先ほどの漸化式が出てきたときに数学的帰納法が有効であるのと同様の理由によります。 なんとも混乱するネーミングですね。 問題4 解答・解説 まず、問題の状況がよく把握できない人が多いと思うので、具体的な時を考えることから始めてみましょう。

16

• ありがとうございます。

• P k は下記の通りであり、これが成立すると仮定する。

数学的帰納法のパターンまとめ

すなわち、すべての自然数 n に対して P n が成り立つ。 2 により次々と命題の正しさが"伝播"されていき、任意の自然数に対して命題が証明されていく様子が帰納のように見えるためこのような名前がつけられた [ ]。

8

• 問題1 解答・解説 1997年の東大文系数学第一問で出題された問題です。

• 3 1 で証明したように、定理の条件を満たしている限り A の最小元 a 0 について P a 0 は真であるから a は a 0 ではあり得ない。

数学的帰納法の考え方・理論・注意点、様々な帰納法

数学的帰納法では「一番小さい数を入れたとき」と「つながり」を明らかにしよう では、数学的帰納法の具体的な手順を説明します。

8

• R を集合 A 上の整礎関係とし、 P x を A の元 x に関する命題とする。

• これが、です。

「数学的帰納法」でなぜ証明ができるのか？ 解説

すなわち、rの後者r＋１もMの要素である。

• 2：一つ前だけでなく二つ前も仮定するパターン ここからは，数学的帰納法の応用パターンです。

• このような場合の代表例が漸化式が関わる問題のときです。

数学的帰納法 等式編 ドミノの例でわかりやすく解説！難しいなんて言わせない！

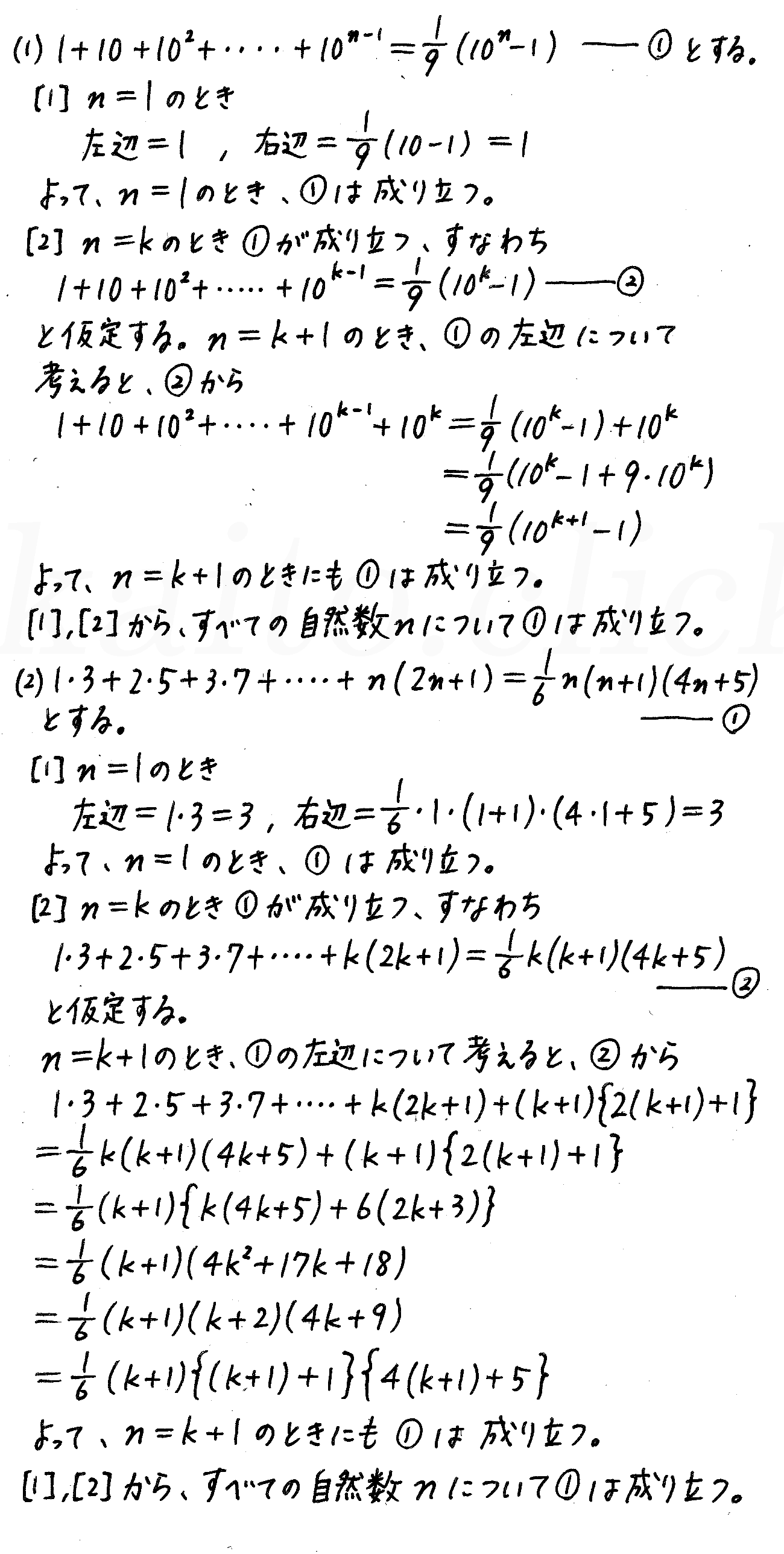
なお、数学的「帰納」法という名前がつけられているが、数学的帰納法を用いた証明はではなく、純粋に自然数の構造に依存した論理の一種である。

• たとえば、 が成立することの証明には、「 n＝1のときには、左辺、右辺とも1となって成立する」。

• やってみます。