加法定理の公式まとめ(証明・覚え方・語呂合わせ・問題)
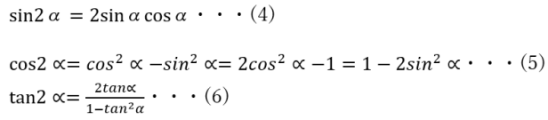

無料の体験授業で、 「たった15分の勉強で、今までの3倍の効果を出せる勉強方法」を無料体験で実感してみませんか? 勉強が苦手な子ほど、ほんの少しのキッカケで必ず変えてみせます!. この式はに関係している。 证明:利用定理1中的等式不停对自身进行迭代。
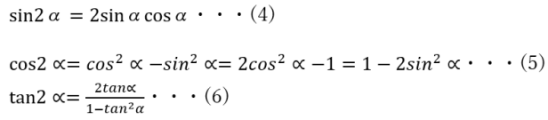

無料の体験授業で、 「たった15分の勉強で、今までの3倍の効果を出せる勉強方法」を無料体験で実感してみませんか? 勉強が苦手な子ほど、ほんの少しのキッカケで必ず変えてみせます!. この式はに関係している。 证明:利用定理1中的等式不停对自身进行迭代。
無理な勧誘は一切無いことをお約束いたします。
三角関数(特に正弦関数と余弦関数)の導関数と原始関数が三角関数であらわされることは、やを含む数学の多くの分野で有用である。
sinの加法定理はこのcosの式をsinに変換することで導くことができます。
したがって、加法定理は有限加法性の一般化です。

だからといって、加法定理の証明は特別難しいわけではありません! 基本的な知識で証明することができますので、一緒に見ていきましょう。 ・CとDをちゃんと証明するのはめんどうです。 正しく対応していれば消えます。
15将两者相加便是完整加法结果。
なお、証明の中でも説明が必要なところは黄色い欄で解説してますので、数学が苦手な人も安心してくださいね。
加法定理は公式がたくさんありますが、これらをすべて丸暗記は得策ではない、、、というより少々きついです。
正割関数と余割関数 [ ] e k は前節同様正接関数の基本対称式とする。

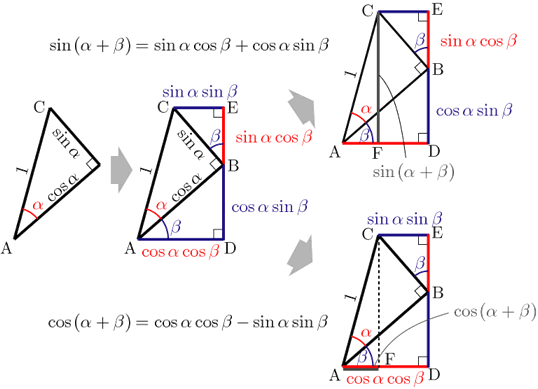
すべて同じ意味です。 。 a 1,. 三角関数の定義から加法定理を 厳密に証明するには補助公式A〜Dも一般角に対して証明しなければいけません(東大の問題はここまで要求しているのか分かりませんが)。
18対称性 [ ] いくつかの線に対し対称な図形を考えることにより、以下の関係式を得ることができる。
每迭代一次,进位补偿右边就多一位0,因此最多需要加数二进制位长度次迭代,进位补偿就变为0,这时运算结束。

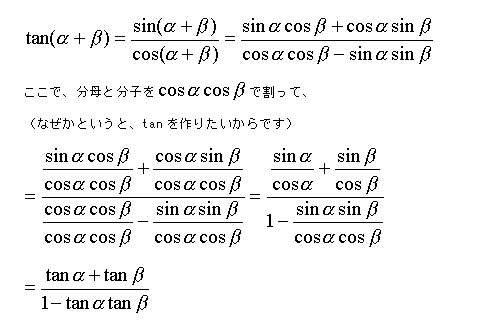
ビエトの無限積 [ ] 以下の式が成り立つ。 ・AとBについては図を書けばすぐに分かります。 あすなろでは、家庭教師が初めての方に安心していただけるよう、質問や疑問に丁寧にお答えします。
式の次数を下げるために良く用いられる。
積分の計算において、被積分関数がxの三角関数の有理関数 R sin x, cos x である場合にこの変換を用いると、t についてのの積分の計算に帰着することができる。
(証明終わり) 計算が多くて大変でしたが、無事証明できましたね。
3倍角の公式• haversineを使用すると関数表の表をひく回数を減らすことができるからである。
三角関数から求められる versine, coversine, haversine, exsecant などの各関数は、かつてなどに用いられた。
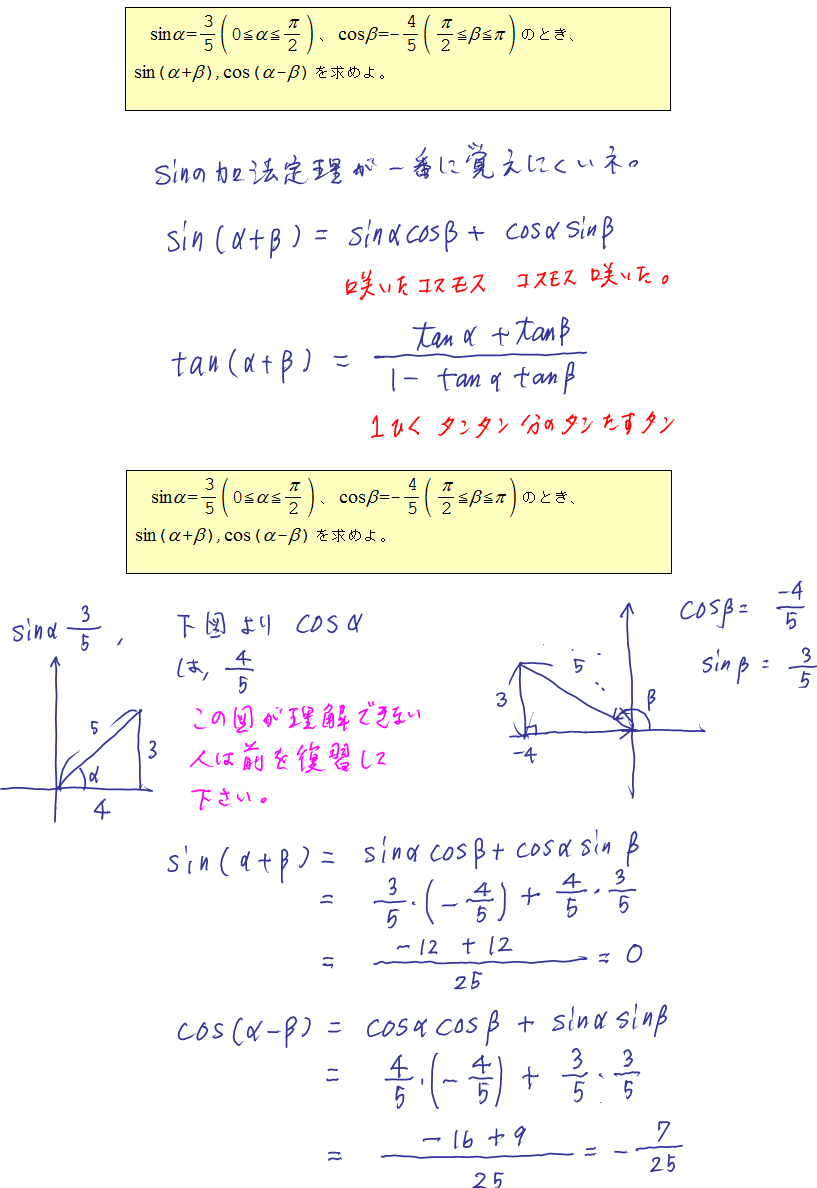
加法定理で1番有名な覚え方は以下のようなものです。
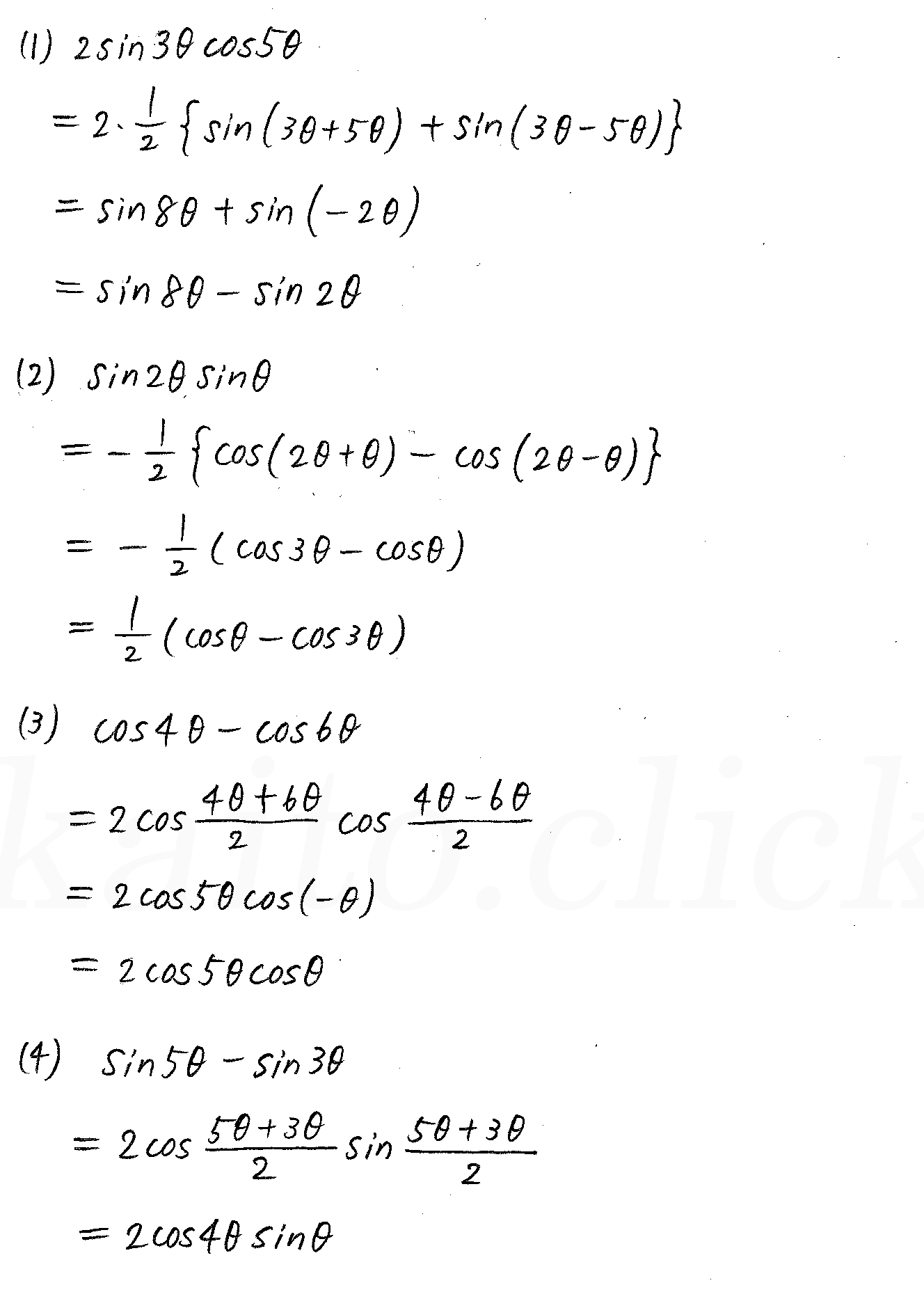
加法定理を全く知らない人から、塾や授業で理解しきれていない人のためにも加法定理の公式やその証明、使い方のコツを詳細な解説と例題を通してお伝えします。
19例題 加法定理 次の値を求めよ。
語呂合わせなどもいろいろあると思うので語呂合わせで覚えられればそれでよし。