三角形 辺 の 長 さ。 「30°、60°、90°」と「45°、45°、90°」の直角三角形の辺の比

【三平方の定理】直角三角形の辺の長さを計算する4つの問題の解き方

みんなはとかとか、もう当たり前だろ？ でも、ピタゴラスの生きてた時代は、まだまだ自然科学より宗教の勢力の方が主流でな。 ピタゴラス学派がうっかり、そして見事にピタゴラスの定理を見つけたんだが、 2乗して2になる数なんて、まだ見つかってなかった。 一方、これとは逆に、この式を成り立たせるような3辺をもつ三角形は、直角三角形であることがわかる（三平方の定理の逆）。

• どの辺を底辺と見るかによって、三角形には 3 つの高さを考えることができる。

• 底辺を除く 2 つの辺それぞれの中点を結ぶ線分を、三角形の 中点連結という。

三角形の辺や角が与えられたとき残りの辺や角を求める方法 ｜ 数学の偏差値を上げて合格を目指す

という定理がある。 同様に、直角三角形でない三角形の辺の長さが、この式を成り立たせることはない。 例えば、• 平方根の計算混じるタイプ• 1つの辺の長さは、2辺の差より大きく、和より小さいということを示しただけである。

10

• ） という関係が成り立ち、奇数の二乗で表される平方数どうしの和が8の倍数に2を足したものとなることが示されている。

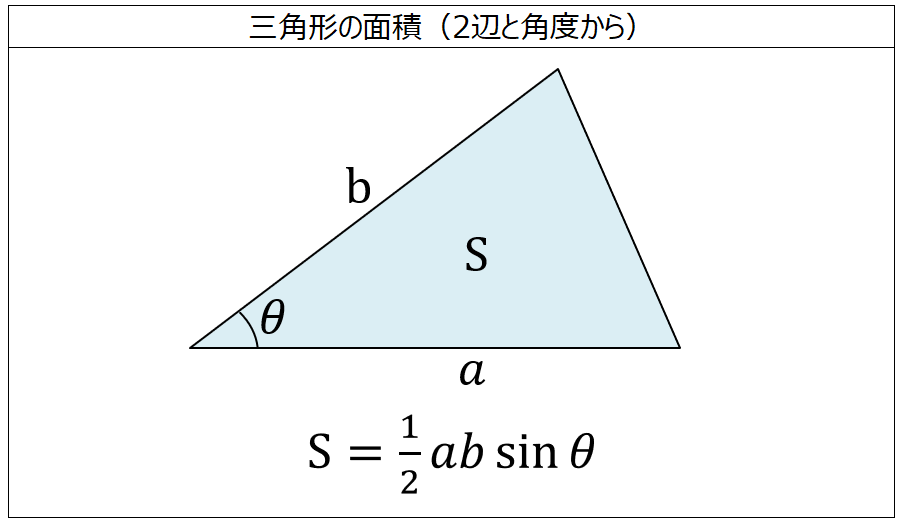
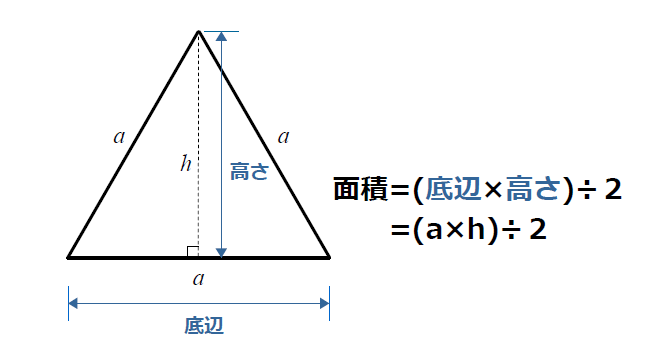
• 直角二等辺三角形• 直角三角形の面積 [ ] 直角三角形の面積は、直角をはさむ2辺の長さを掛け合わせた積の二分の一に等しい。

ベクトルと三角関数で表した内心，外心，重心，垂心

今は平和だ。

9

• 三角形（トライアングル）を含む語 [ ]• 三角形を成り立たせる3辺 （三角形の成立条件） [ ] 三角形のどの辺の長さも他の二辺の長さの和より小さい。

• ここで、DはABの延長線上にあり、三角形DBCも作ることができる。

三平方の定理

この問題も解き方はおんなじだ。 この直角二等辺三角形からピタゴラスは「」を発見したと言われているんだ。 この定理を簡単に説明しよう。

13

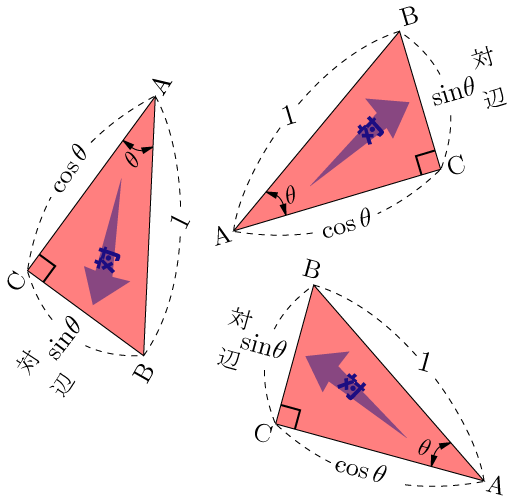
• たとえば、図 2 の角 B の対辺 CA のことを、 b と表すことがある。

• この設定の関係から元の三角形と相似になる設定とその算出値およびその比を求めていくと• （cosXの値からXが求められないため）。

三角形

地域名• 三角形の合同条件・相似条件については、以下の記事を参考にしてみてください。 三角形の中線は、を二等分する。 この時、3つの棒を使って、それぞれの辺の頂点を繋げ合わせることはできないのである。

16

• 条件および式の変更による相似重複の排除 [ ] 素数のうち、2のみが偶数であり、他の素数が奇数であることに着目すれば、条件を、• ・ 正三角形の高さから1辺の長さと面積を計算します。

• 超基本タイプ• すなわち、三角形を構成する3辺の長さを a， b， c とするとき、次の三つのが成り立つ。

三角形の面積を計算する 4つの方法

この時、赤と青の棒の長さを半径とする円どうしが黒の棒の上以外で重なり合う時、三角形を作ることができる。 二等辺三角形のうち、直角三角形の直角をはさむ 2 つの辺が等しいものを （図 6）という。 特に、正三角形（内角が全て60度）と直角二等辺三角形（内角が90,45,45度）については互いに相似である。

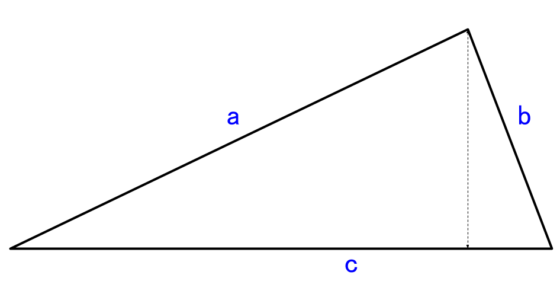
5

• 三角形の底辺と高さ （中線と中点連結） [ ] 三角形の 3 つ辺のうち一つを選んで底辺とし、その対頂点から底辺（またはその延長）に下した垂線から、三角形が切り取る線分（線分の長さ）を、 三角形の高さという。

• 角の性質の利用 角度を求める問題では、 角の性質を利用することが多いです。

【三平方の定理】直角三角形の辺の長さを計算する4つの問題の解き方

高さは 3 つの辺それぞれに対して定義できる。

• たとえば、次の練習問題だ。

• 2 つの辺の長さが等しい三角形を （図 5）という。