二 等辺 三角形 角度。 二等辺三角形
二等辺三角形・直角三角形の定義:合同条件と証明問題

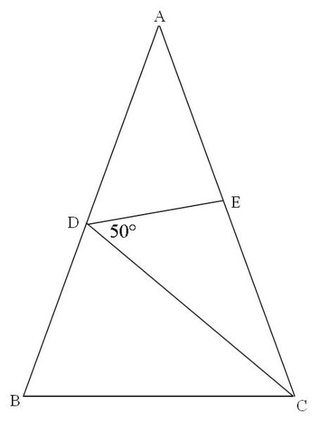
三辺比相等(三辺の比相等) 対応する3組の辺の長さの比が等しい 二辺比夾角相等(二辺比挟角相等・二辺の比と夾角相等・二辺の比と挟角相等) 対応する2組の辺の長さの比と、挟まれる角の大きさがそれぞれ等しい 二角相等 対応する2組の角の大きさがそれぞれ等しい 「三辺比相等」は、ある三角形と、また別の三角形について、対応する辺の長さがそれぞれ等しいことである。 底辺の対頂点を通る、底辺の平行線を引くとき、平行線の間の距離は三角形の高さに等しい。 特に、正方形を 1 本の対角線で 2 つに分けると、直角二等辺三角形が得られる。
6
二等辺三角形の定義と性質をサクッと確認しておこう!
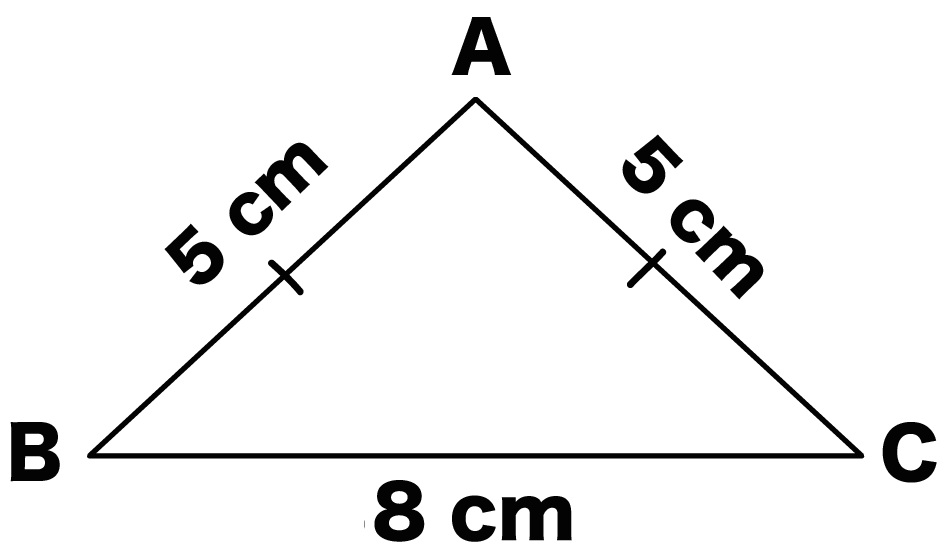
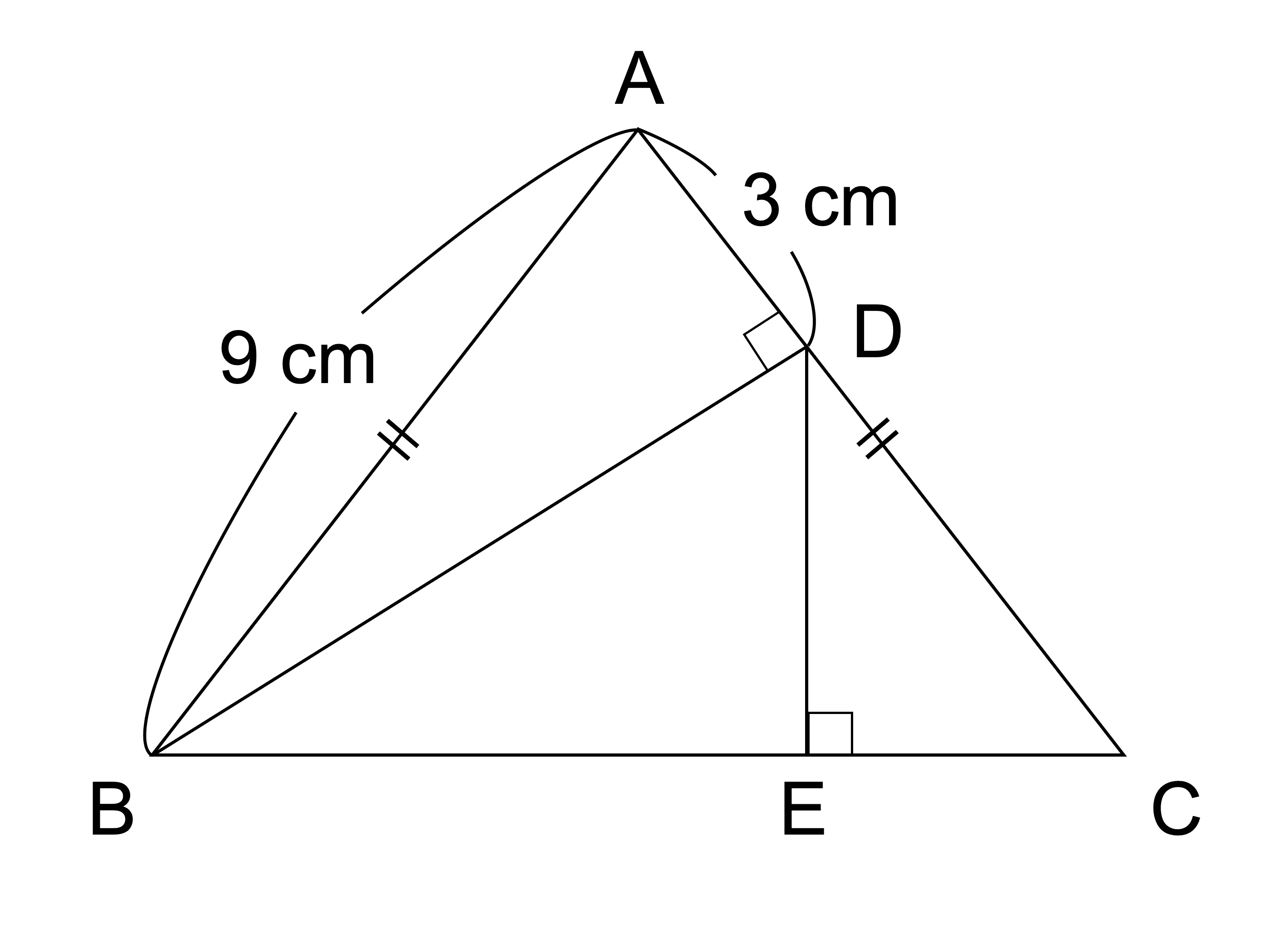
二等辺三角形• 一般的な三角形には斜辺がありません。 二等辺三角形だと2つの辺が等しいと同時に、必ず底角が等しくなります。 底辺と垂線が交わる点をCとするとき、辺の長さAC=BCです。
4
二等辺三角形の底辺は?1分でわかる意味、長さの計算、角度、高さ、三平方の定理との関係


この定理としては、 底角が等しいことがあげられます。 二等辺三角形と直角三角形の両方の性質を理解していないと問題を解けないケースが多いです。 そこで点DがBCの中点となる以下の二等辺三角形を考えましょう。
二等辺三角形


よって底辺の長さは です。
9
直角二等辺三角形の辺の長さは?1分でわかる求め方、公式、辺の長さと角度の関係、証明
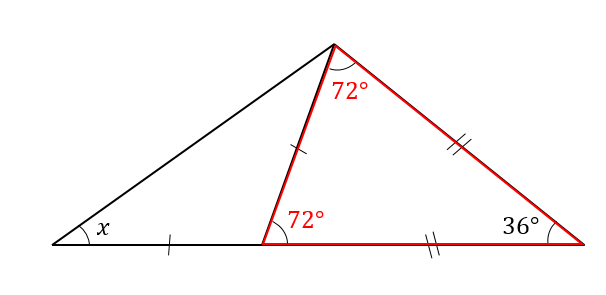

実際に直角二等辺三角形の長さを計算しましょう。 二等辺三角形のうち、3 本の辺の長さが全て等しい三角形はという。
3
二等辺三角形とは?定義や定理、角度・辺の長さ・面積の求め方
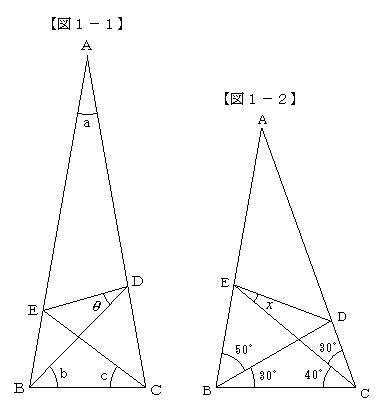

それぞれの角度は、30度の直角三角形と45度の直角二等辺三角形です。
7
直角二等辺三角形の辺の長さは?1分でわかる求め方、公式、辺の長さと角度の関係、証明
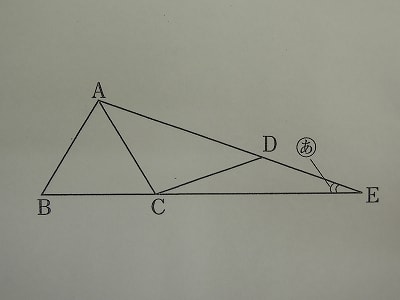
相似条件 [ ] ある2つの三角形について、以下の条件のうち1つでも満たしていれば、その2つの三角形はである。 底辺の中点と、対頂点を結ぶ線分を、三角形の 中線という。
10
直角三角形の斜辺は以下の部分を指します。
意味が理解頂けたと思います。
三角比(30°,45°,60°)|もう一度やり直しの算数・数学

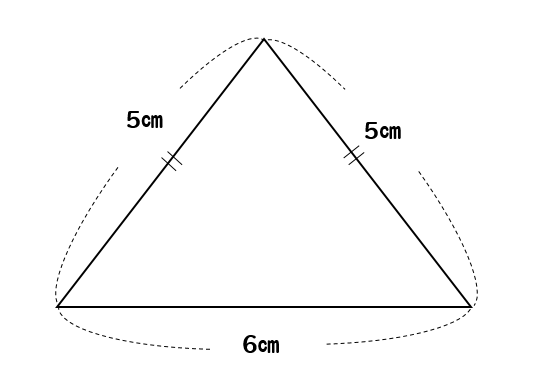
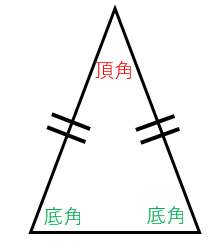
二等辺三角形の性質としては、2つの辺が等しく、かつ底角が等しいです。 頂角がである二等辺三角形はとよばれる。 また底辺の両端にある角を「底角(ていかく)」といいます。
6
二等辺三角形
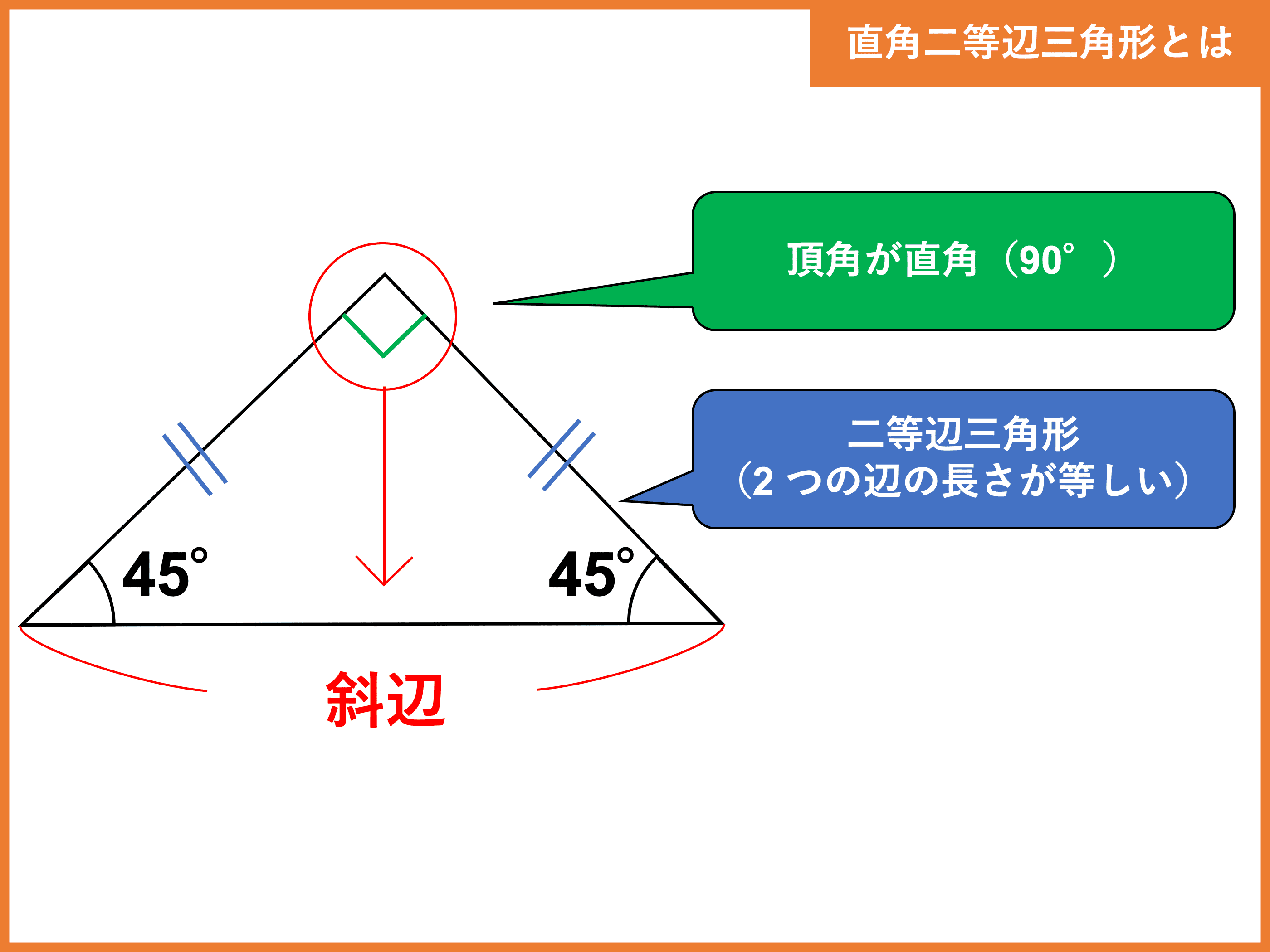

まとめ 今回は頂角について説明しました。 直角二等辺三角形の辺の長さの公式と証明 直角二等辺三角形の公式を簡単に証明します。
17

















