偏差値とは何か?

分散を求める 分散は、テストの得点がどのくらい散らばっているかを示す値です。 偏差値の注意点 偏差値は、「平均点との差」と「得点のばらつき」の両方を踏まえたうえで、自分がどの程度の位置にいるのかを表した数値ですが、テストを受けた人数が少ない場合は、利用する価値が低くなります。 これはこの後にも何度か登場するのできちんと意味を理解しておいてください。
11

分散を求める 分散は、テストの得点がどのくらい散らばっているかを示す値です。 偏差値の注意点 偏差値は、「平均点との差」と「得点のばらつき」の両方を踏まえたうえで、自分がどの程度の位置にいるのかを表した数値ですが、テストを受けた人数が少ない場合は、利用する価値が低くなります。 これはこの後にも何度か登場するのできちんと意味を理解しておいてください。
11それ以外にも、 偏差値はグループ全体の位置なので、 周りの子がサボったら、 あなたの偏差値は相対的に上がる ということです。
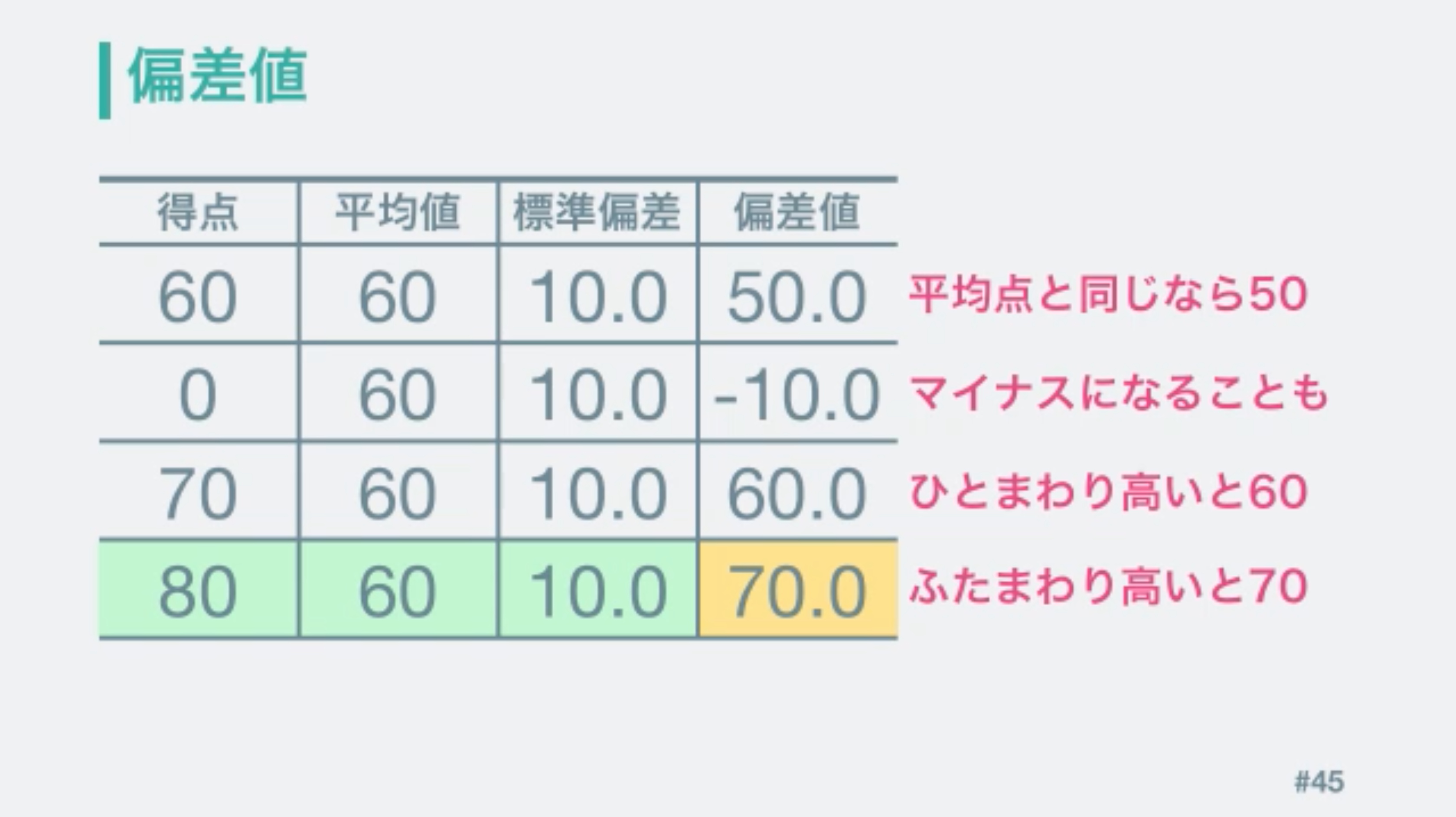
たとえばあなたが、社会で60点を取ったとします。
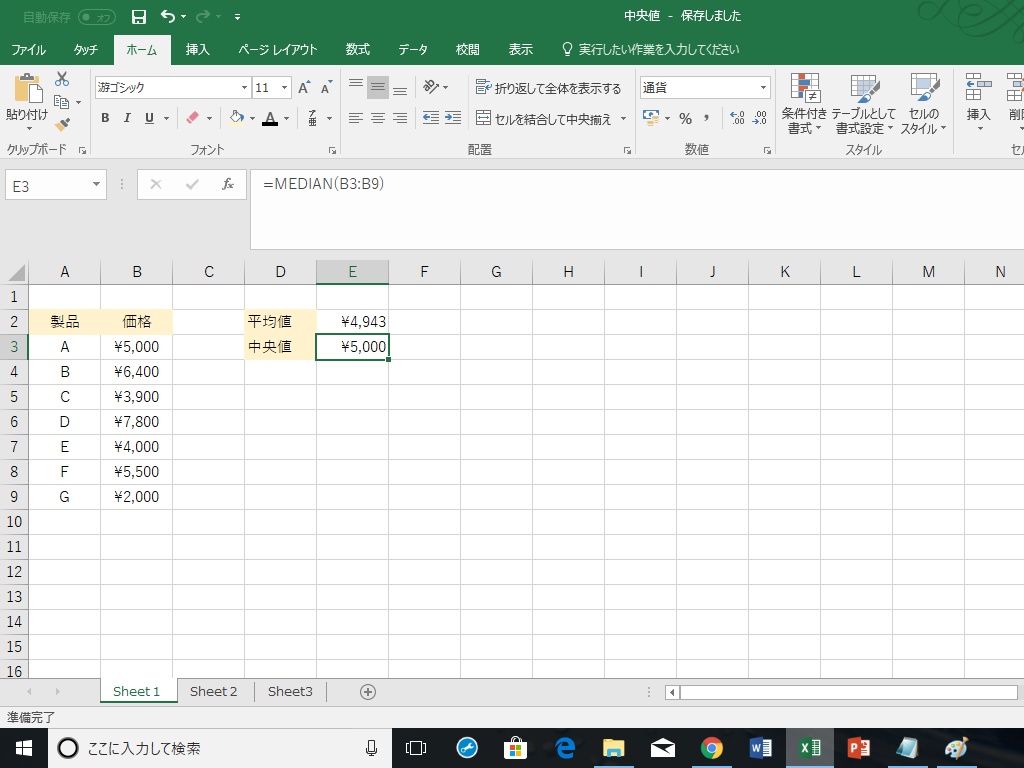

スポンサーリンク. その時の社会の平均点が70点だとしたら、 偏差値は約45になるということです。 平均点を求める• 一方、得点が分散しているテストでは 平均点から離れた得点を取りやすく、平均点以上の得点であっても偏差値はそれほど上がりません。
点数だけ見ると数学が悪いようにみえますが、平均点が英語92点、数学55点の場合、数学の方が偏差値は高くなります。
平均点も同じだとしても、学年の点数がどのように分布しているかによって評価が変わってきます。

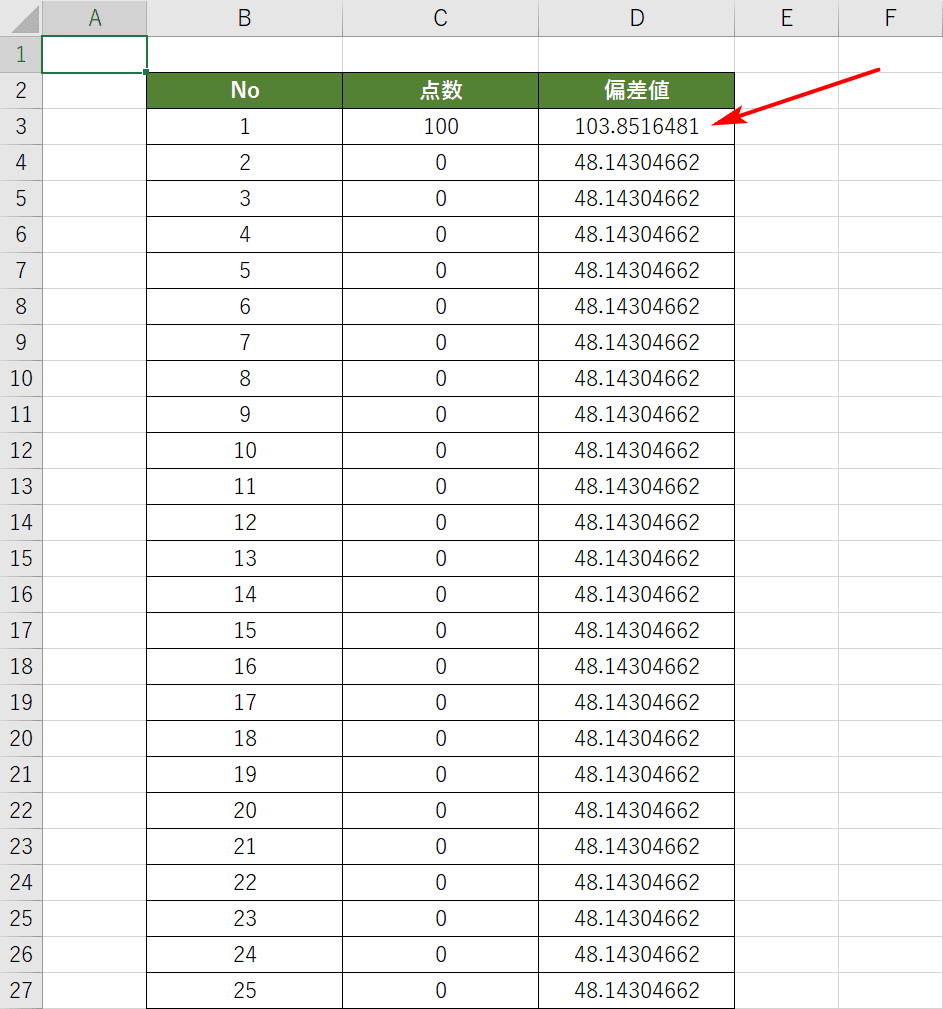
以下の値で求められます。 そのため母集団となる人数が少ないと、あまり偏差値を利用する価値がありません。
よく、偏差値と点数はどう違うの?という質問を受けることがありますが、分かりやすく説明すると下記のようになります。
高校受験の合格率を判断する偏差値は、 学校内ではなく、今年受験をする中学3年生 すべての中での偏差値になります。

このように、テストで同じ点数をとったとしても、その人の 実力はわかりません。 志望校ごとの受験者の成績や入試の定員などの様々な要素をまとめて、偏差値を算出します。
15このように、単に得点や順位の比較だけでなく、 平均点の異なるテスト間の成績を比べることができるのも、偏差値ならではの特長なのです。
試験の話で言うならば0点~100点の人が幅広くいる場合、標準偏差が大きくなります。
(クリーム色の部分) 「分散」とは,このクリーム色の部分の,平均を求めるだけです。 13だったので、おおむね合っていると言えるのではないでしょうか。
偏差値は統計学に基づいて公式化されており、学力判定などに用いられます。
偏差値のメリットは、点数や順位に左右されず、集団の中で自分の学力がどれくらいの位置にあるかを知ることができることなのです。

よって、データのばらつきを評価するときには、分散よりも 標準偏差の方が直感的にわかりやすく、よく用いられやすいといえます。 分散を求める 分散は、テストの得点がどのくらい散らばっているかを示す値です。 (このとき,自分以外の人の偏差値は48です。
11【テンプレートあり】エクセルを使えば簡単に偏差値を計算できる 偏差値や標準偏差、下方偏差などを求めたい場合、計算式は全て公式化しています。
偏差値と通知表の評定の見方は、 相対評価ではおおよそ偏差値35までが「1」、35~45が「2」、45~55が「3」、55~65が「4」、65~が「5」となっていました。


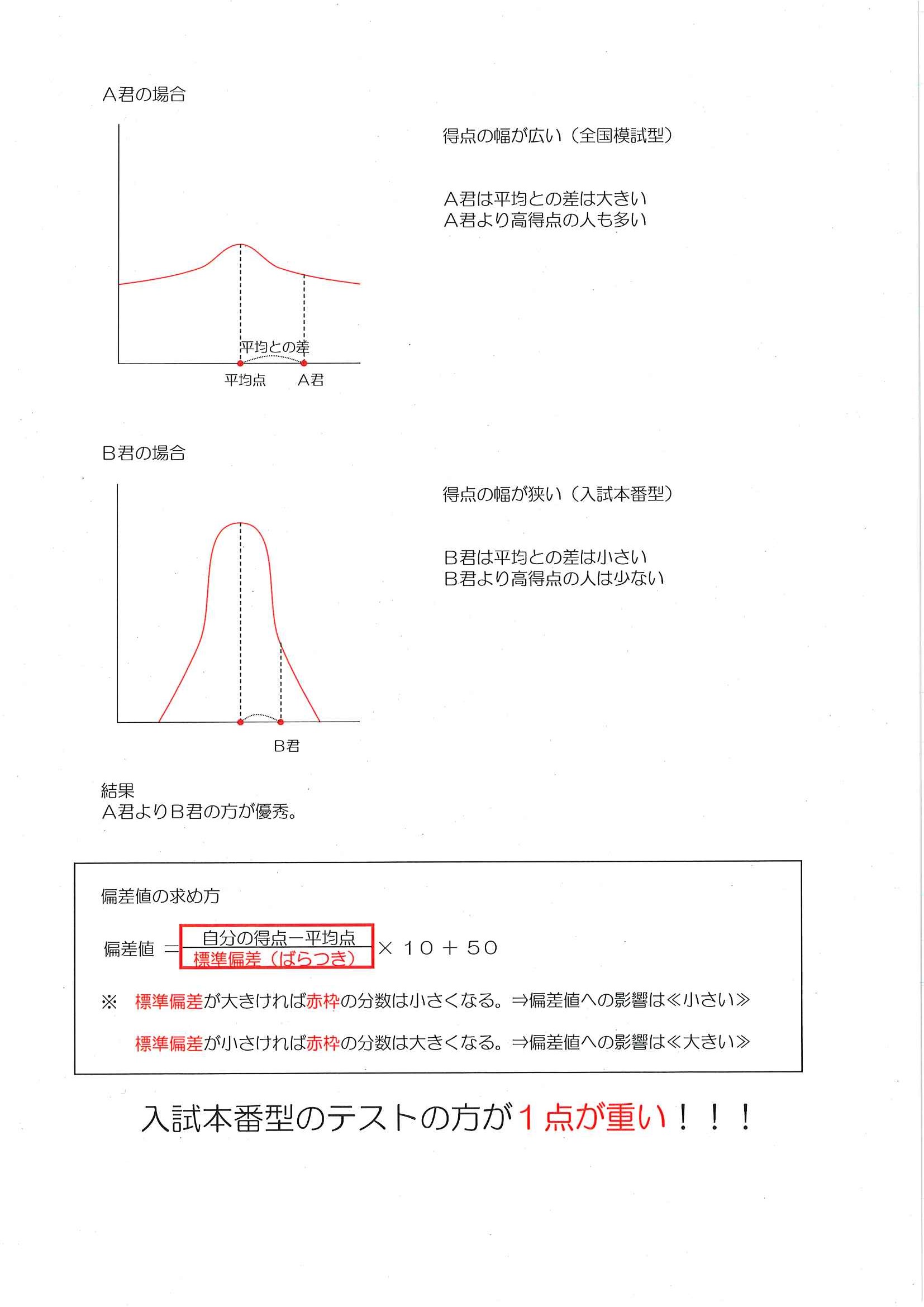
偏差値は ・平均との差 ・標準偏差の大きさ で決まります。 ここには駿台の偏差値は非公開となっており、ありませんが、 駿台全国模試のように、国公立大学~東大・京大を目指す人、つまり 学力上位層ばかりが受ける模試では、 学力差は小さくなるため、 上位層と下位層の差は小さくなります。
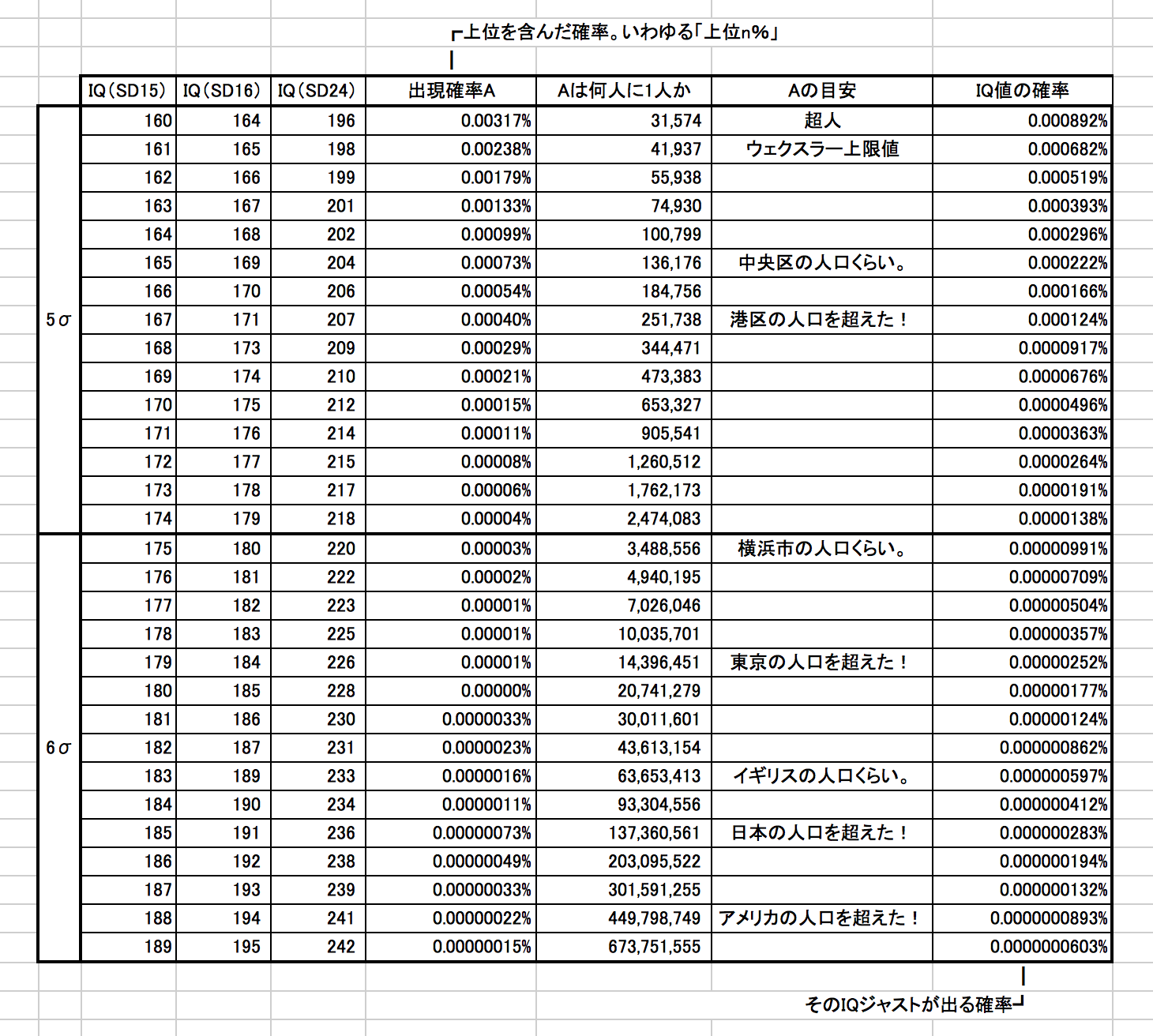
6偏差値を計算する上では、 上記の曲線のように点数が分布している、と 想定していますよ、 ということになります。
「点数 — 平均点」をだす つぎは、 受験者の点数から平均点をひいてみよう。

そのため、 あなたが勉強をさぼっても、 他の受験生がそれ以上にサボったら、 合格できるのです。 偏差値の出し方を説明する前に、まず偏差値とは何か?というところからお伝えします。 このように、自分の点数とまわりの平均点を伝えれば、正確に自分の実力を表現することができそうです。
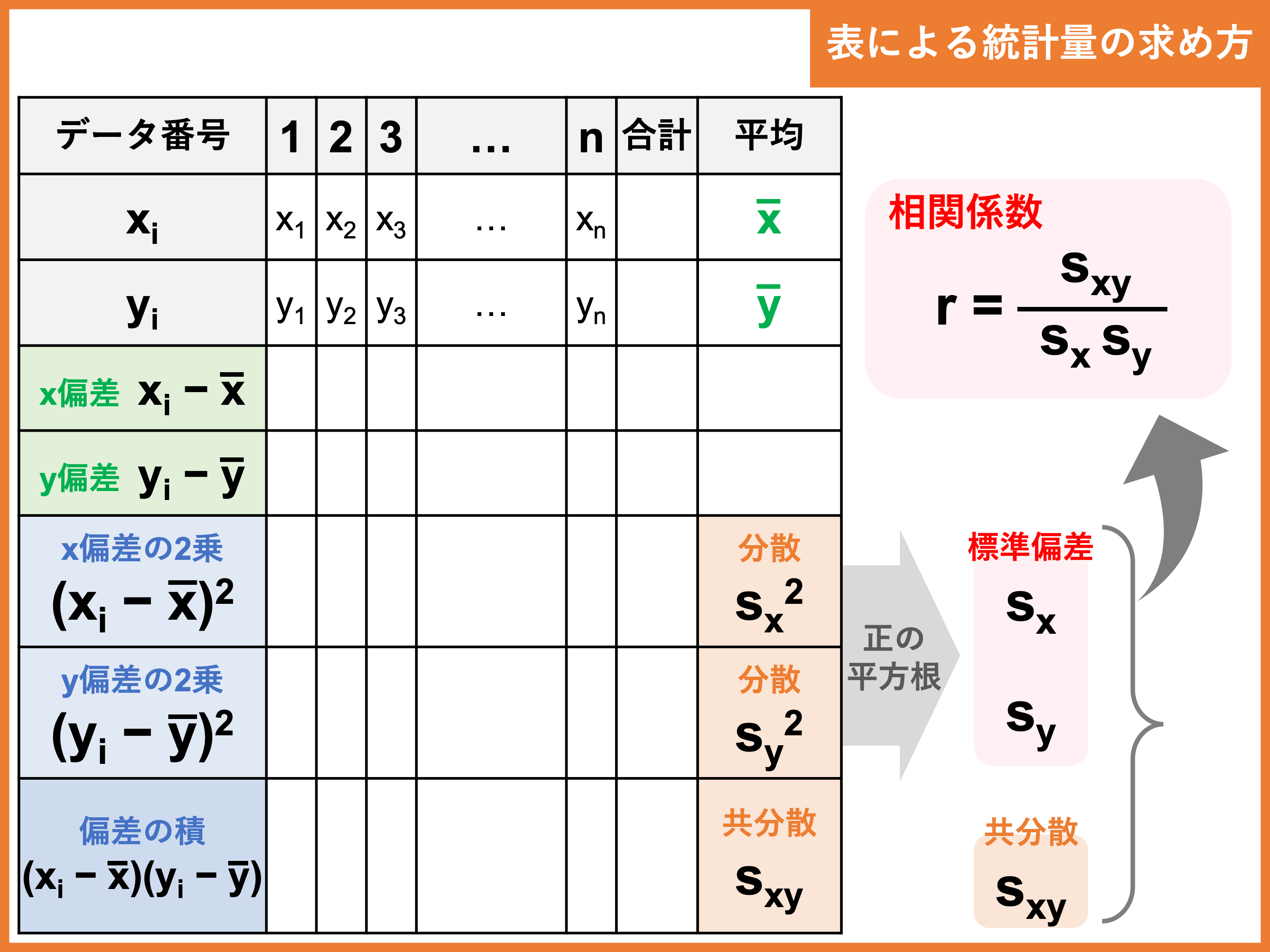
両者の最大の違いは、 標準偏差が分散の正の平方根であることです。
このテストは、あなたを含めて10人の生徒が受験しました。
逆もまた然りです。 氏名 A B C D E F G H I J 得点 50 90 60 60 40 100 40 40 50 70 平均点 との差 10 30 0 0 20 40 20 20 10 10 の平方数 100 900 0 0 400 1600 400 400 100 100 平均点:60 分散:400 標準偏差: 5.標準偏差を求める またまた耳慣れないことばが出てきました。
6試験を行うと、平均点や、受験生ごとの得点のばらつきが発生します。
標準偏差が大きい場合は正規分布曲線のすそ野が広がり、小さい場合には中央に集中してとがったかたちになります。