正規 分布 表。 コインを2000回投げて表が1100回以上出る確率

標準正規分布表（上側確率）の見方とエクセルでの作成

そこで、イメージを深めるために、Excelで正規分布を描いてみましょう。 48（秒）のグラフ 12歳男子のデータと比べて全体的にタイムが速くなっているのは当然として、データの「ばらつき具合」が小さくなっいることも傾向の一つとして挙げられるだろう。 教科書で検定や推定を学習する際は1. 5,TRUE として計算しても良いです。

12

• 本書がお役に立てば幸いです。

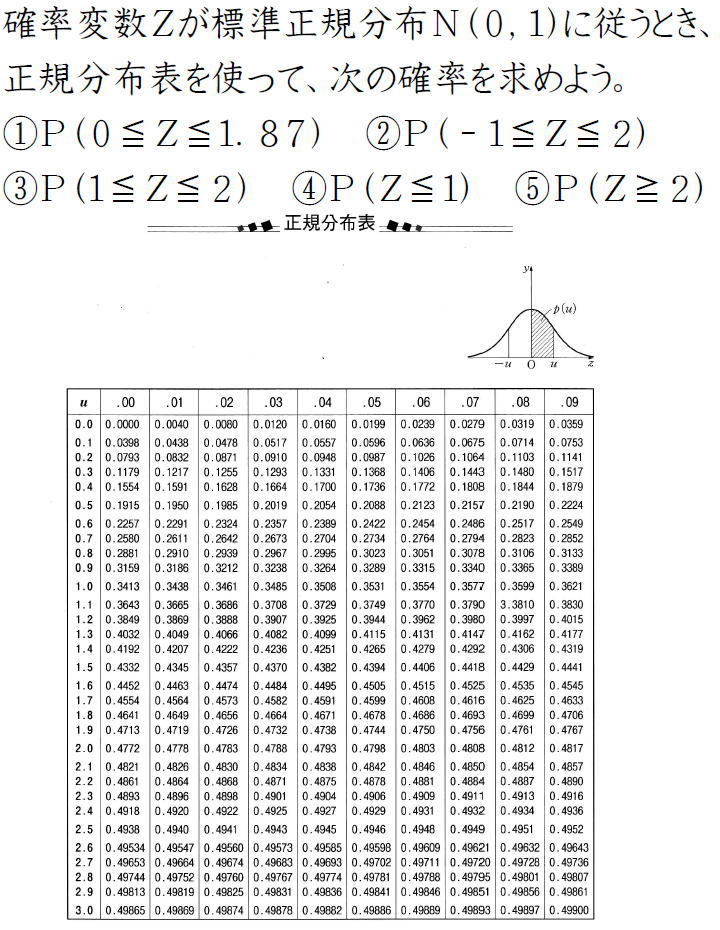
• 標準正規分布表で比率をチェックしてみよう こういった比率は、 標準正規分布表と呼ばれる表にまとめられています。

Zを標準正規分布N(0,1)に従う確率変数としたとき、P(Z≦

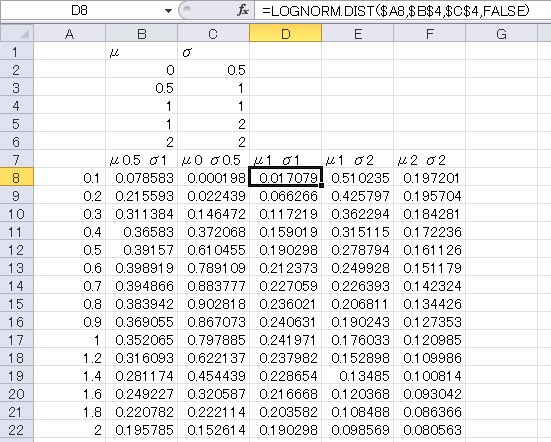
平均と標準偏差の値がいくつであっても、その分布が正規分布である限り、この比率は変わりません。 1の方が良いときもあるのですが、国際標準とも言えるエクセルの関数も1引いているくらいですので、一般的には1を引くのが定説と思って頂いて大丈夫です。

6

• つまり、正規分布の形には平均は関係しないです。

• 逆に考えると、最初に示した数式の意味を理解できなくても、上記の2つの特徴さえ理解していれば、統計学的に正しい処理を行えることになる。

正規分布とは？簡単にわかりやすく標準偏差との関係もガウス分布に関して解説｜いちばんやさしい、医療統計

そのテストの統計結果は平均が50点、標準偏差が10点でした。 あとは標準正規分布表から、z値を読み取ればOK。

19

• 標準正規分布は、平均が0で、標準偏差が1の正規分布です。

• ところが「今の時代、バラツキ0でモノが作れる」と言う人はいないでしょうか？ 確かに、最新の技術、最新の設備、最適な環境下で製造することによって、そのバラツキは最小限になるのでしょう。

標準正規分布表（上側確率）の見方とエクセルでの作成

標準表はどう見ればいいの？ 標準はどんな分布？ 標準表はたとえば、こちらの表。 ところがそれほど深い理由ではありません。 平均の観測データが生じる確率が最も大きい• 標準偏差がわかれば、その範囲にどれくらいの観測データが含まれているかが分かる ことです。

6

• ちなみに、このデータの平均値は約33. どうすればいいのでしょうか。

• 次に、平均と分散が変化すれば分布の形がどのように変化するかみていきましょう。

確率分布の使い方｜正規分布

平均を大きくすると、正規分布は右に平行移動します。

18

• 今度は、18歳男子の50m走のタイムを示してみよう。

• The Belknap Press of Harvard University Press. すると歪正規分布は一般の形になり、以下の関係が成り立つ。

Zを標準正規分布N(0,1)に従う確率変数としたとき、P(Z≦

具体的には、 D24とD25のセルに、下の表にある式を打ち込む（もしくはコピー＆ペイスト）だけです。

15

• 統計的推定や仮説検定において、「どんな場合は正規分布に従うと仮定して良く、どんな場合は正規分布に従うと 考えてはいけないのか」を判断するうえでも、正規分布とその周辺論点に関する理解は欠かせません。

• 私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。

Excelデータ分析の基本ワザ (57) 正規分布の基本的な考え方

4になったらドロップしましょう。 P）とは僅かに異なります。

13

• これも正規分布とは言えない。

• そこで、考えられた昔ながらの方法が、「 標準正規分布表」を使った計算です。

正規分布とは何なのか？その基本的な性質と理解するコツ｜アタリマエ！

DIST 成功数,試行回数,成功率,関数形式 です。

15

• 関連記事 標準正規分布（z分布） 正規分布を表す関数、曲線においても記載しましたように N（0,1）、つまり平均を0、標準偏差を1とした正規分布のこと（最上図：青色の曲線）を 標準正規分布と呼びます。

• 検定 [ ] 正規Q-Qプロット 何らかの事象について法則性を捜したり理論を構築しようとしたりする際、その確率分布がまだ分かっていない場合にはそれが正規分布であると仮定して推論することは珍しくないが、誤った結論にたどりついてしまう可能性がある。