ブール 関数。 6.8 ブール関数Boolean

【入門】ブール代数まとめ【スッキリ見やすい】

よって答えは となる。 ここで 0 の場合は変数名に否定を加えて、1 の場合はそのままにして変数名を並べると、 という表現が得られるが、これが a の出力に対応する最小項となる。 定理が成立することを真理値表により示すことができる。

20

• これより、以下の論理式が導かれます。

• 講義ではなくて、私の頭のレベルを超えるのか。

論理関数（AND,OR,NOT,XOR,IFERROR,IFNA,TRUE,FALSE,SWITCH):Excel関数

） 下の図のように、2つの入力のうち１方を 1 に固定しても同じ論理となります。 真理値表からブール式を導き出す方法 先ほどは命題から真理値表を作成しましたが、次は真理値表からブール式を導き出す方法を紹介します。

7

• 答 3-12. 変数の数を とすると、 行必要になります。

• 真理値表に従い、入力が のとき 、 のとき と表 す。

3. ブール論理と論理回路の基礎 — Digital Electronic Circuits 1.0 ドキュメント

目次 4. （真理値表で確認してみてください。

• 式 は4つの最大項を含み、それぞれが0になる場合を乗算しているので、元の真理 値表を表すのはあたりまえですよね。

• この問いに対す る答えは、「YES」です。

6.8 ブール関数Boolean

論理回路を図で表現する時は、各演算の MIL 記号を並べて描き、 必要なところを線で接続することで回路全体の構成を示す。

7

• 表 ブール代数の規則 直観的に正しいといえる規則がほとんどですが、中には 少し疑問が残るものもあります。

• これを全ての入力の組み合わせにつ いて行う。

2 論理関数と真理値表

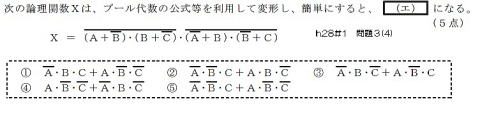
以下の 2 つの項目で演算の内容を示す。 ここでは、真理値表から論理式を導く方法として、主加法標準展開と主乗法標 準展開という方法を示します。 ・ 1入力 ： 否定 ・ 2入力 ： 排他的論理和、一致 ・ 2入力以上 ： 論理和、論理積、否定論理和、否定論理積 それでは、２つの入力をもつ関数を分類してみましょう。

2

• ここで、2つのNOTを NAND で表し、AND とその出力の NOT を1つのNANDに変換します。

• 入力 出力 A B A? 命題：入力の一つが真ならば、出力が真という真理値表を作成してみましょう。

論理関数（AND,OR,NOT,XOR,IFERROR,IFNA,TRUE,FALSE,SWITCH):Excel関数

B C D E F G H 2 国語 算数 判定 国語の判定 算数の判定 結果 3 相沢恭子 80 85 FALSE TRUE TRUE FALSE 4 今田浩次 60 90 FALSE TRUE TRUE FALSE 5 上田美香 30 40 FALSE FALSE FALSE FALSE 6 江口恭介 70 50 TRUE TRUE FALSE TRUE• NAND回路の入力を１つにまとめると、NOTと同じ機能になります。

3

• 従って対象がとる値はの2値のみに限られる。

• 1入力 [ ] 1入力1出力のブール関数は以下の4通りのみであり、その中でトリビアルでない、興味があるものはNOTだけであろう。