【中学2年生】平行四辺形の定義と性質

対角の大きさが等しい(対角は2組あるが、いずれもこの性質を満たす)。
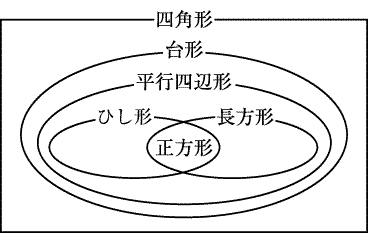
3縦と横の長さが異なる長方形、平行四辺形はひし形では無いです。
納得できないですね! 「証拠は?」となりますね。

「なぜ平行四辺形の向かい合う2組の辺は平行なのか?」と問われたら、 「そのような四角形が平行四辺形と定義されているから」という答えになってしまいます。 2組の向かいあう辺が、それぞれ平行な四角形. 証明は対角線によって、平行四辺形を2つの三角形に分け、その三角形の合同を示すことでできます。
5これらのことは定義から容易に証明可できます。
平行四辺形とは、「 2組の向かい合う辺 対辺 が、それぞれ平行な四角形」のことを指します。
定義、定理、性質、特徴、違いは? 定義 … 意味をはっきり述べたもの 証明の根拠である 定理 … 正しいと証明されたもの 証明の根拠になれる 特徴 … 他のものと違って、特色がある 特長 … 他のものよりも、特に優れている 性質 … もともと持っている特性 性格 … 変わる可能性を含んでいる特性 となっていますが 数学のテストで「言葉の意味を述べよ」などは出題されないと思いますので、 ・定義 … 「だから、そういう名前をつけた」 で十分ですね ex 「茶髪. そいつは、平行四辺形じゃない。
質問者さんの書かれた「条件」は、どういう意味で使われているのかはっきりしませんが、もし定義のつもりでしたら、質問者さんの言われる「性質」とは違います。
また、平行四辺形は 台形の一種です。
脚注 [ ]• ダウンロードしたり印刷したりして、要点を見直すのに活用してください。


関連記事 「平行四辺形の性質」について詳しく知りたい方は 「平行四辺形の証明」について詳しく知りたい方は 3. さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については 長方形が 『対角線の長さが等しい』、 ひし形が 『対角線が直交する』という性質があります。
よって4つの三角形の斜辺、底辺、高さは全て同じになるため「合同」です。
日本語で例えるなら、「皆 みな まで言うな!」「あとは一本道」「自動的に決まる」 将棋で例えるなら、『詰み』の形で終了! 『玉まで取る』ところまでしないですね すなわち、 「決まった後の作業」は、言葉は悪いですが『無駄』ということですね そして、どこまですれば『詰み』なのか、ちゃんと「明記」してくれているのが数学の優しいところですね! そして、それが…「 三角形が1つに決まる条件」ということであり、 2つの三角形が、同じ条件で決まれば「 合同」ということですね! cf. 平行四辺形の性質の証明 平行四辺形の定義を仮定したとき、それぞれの性質をもつことを証明しましょう。

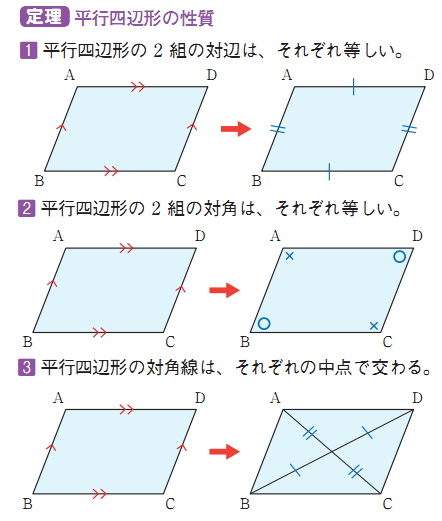
図形の証明の方法は1通りとは限らない。 ・2組の対辺はそれぞれ等しい ・2組の対角はそれぞれ等しい ・平行四辺形の対角線は中点で交わる それぞれ解説します。 ある辺を底辺と決めたら、それとに交わるを底辺からその対辺まで引いたとき、その線分の長さが高さである。
1こんな感じで、 2組の向かいあう辺が、それぞれ平行な四角形 が平行四辺形なのさ。
できた三角形を右側にスライドさせるとピッタリはまります。