信用区間に0が含まれるかどうか、という観点で検定もできる• しかし, だからといって, 理論上の汎化誤差を無視していいというわけではない. 例えば、 Q１．なぜ事前分布を信じることができるのだろうか？ Q２．ベイズ法は数理や理論に支えられていないのだろうか？ 『百人いれば百個の推論』でよいのだろうか？ Q３．私は BIC や DIC でモデルを設計して来たが、それで本当によかったのだろうか？ 他の本には書かれていなくて、本書だけに書かれていることは次の３点です。 つまり、真の確率モデルq x からの無限個のサンプルを集めた際の経験損失は、汎化損失と等価です。
データとの距離（適合度）は、絶対的な定数ではなく、相対的な比較による• 統計学や機械学習の研究が「その場限りの工夫を繰り返して論文数のみ増大し実質的に同じ場所を回り続ける」という 状況を越えて、到達できた場所と未解決問題とを峻別することができる真の実践の学問となるためには、 理論と数理は不可欠です。
ミドリ本の素晴らしいところは、 1. 3つの平均 まず書籍に登場する3つの平均のとり方があって、それぞれ別の意味を持っていて重要なのでおさえておく。
次に標準偏差は、分布の標準偏差で、最尤推定のときの標準誤差と同じような指標です。 A を「患者が病気である」という事象、 B を「結果が陽性だった」という事象とする。 が未知であるからこそ推測するというの問題が発生するので, 事前・事後的のいずれでも正則な条件を満たしているかを知ることはできない. ついでに事後分布は簡単に言えば次のように計算します。
9また真の分布が不明でも、実対数閾値を求めることができます。
こうして、検査結果が陽性だったという条件下で、それが偽陽性である確率をベイズの定理を用いて計算しよう。
私は、今後、イケている風（笑）を醸し出したいならベイズについて語れたほうがいいとは思っています。 実際には真の分布 は不明であるので、サンプル（データ）と事後分布から計算できる量で近似していくことになる。
2これについては、世界中の多くの 統計学者が気づいていなかった点であり（気づいていたとしても正しい理論 は発見されていませんでした 、ベイズ統計学やベイズ学習理論で 世界中で読まれている本にも間違ったまま記載されていました。
しかし、喫煙者に限定した調査を行えば相関性が見つかるかもしれないし、さらに肺癌患者のみを対象とした調査を行えば、肺癌と生活習慣の間にある因果関係の仮説を立てるヒントを得られるかもしれない。
使い慣れた仮説検定と前提が違うので（またわかりやすい有意水準もない）、とっつきにくい• DICはBICと同じように、情報量基準で、絶対値に意味はなく、相対的な大きさを比較するものです。 この時捜索と並行して用いられた手法は次のものであった。 しかし文献によりMAP推定値を用いた方法も含む場合など、さまざまな表記があります。
1真の分布は決まったものなので、定数ですね。
ベイズ交差確認法の分散が汎化誤差の分散と等しいことを示します。
もしも、対数尤度比関数が相対的に有限な分散を持たないと、サンプルの現れ方に依存して事後分布の形状が極端に大きくなり、汎化誤差や自由エネルギーのサンプル（データ）の数 に対する挙動が大きく変化してしまうからである。
近年、ベイズ統計が更なる注目を浴びているのは、コンピュータの性能向上による機械学習、深層学習の進展もあります。
The Belknap Press of Harvard University Press. p E G を、被告人が有罪であるとの条件 G の下で DNA が一致する事象 E の確率とする（これらは通常確率1であると見なされる）。
ですので、まずは、 - - - といった、実際に手を動かしながら統計学を学べる系の本で基礎を学ぶのがいいでしょう。
相転移については４章で説明しています。
確率モデルが一つで近似するような場合、指数型分布が的に非常によい性質を持っているので、どの推測方法を用いても結果には大きな違いはない p. 信頼区間に似た、信用区間も同様に推定できる• 応用例 [ ] 薬物検査 [ ] 薬物検査の例を表す樹形図。 詳しくは下のような記事を参考にしてください！• ベイズ統計学に初めて出会う人が疑問に思うことを解説し，理論的な基礎を明らかにし，実用上で注意することを説明する。 これは , とも書かれ, 個の観測値と事後分布 で決まる, の密度関数である. ベイズ理論とは何か ベイズ理論は、おおまかに言うと「未来を推測するには過去を振り返らなければならない」と要約することができる。
5点推定値は多少不安定だけど、同じように推定できる• データを集めてきたり、くっつけたり、きれいにしたり、あんなことやこんなことをしたり。
そうでない場合には、 正しくありません。
真値がただ一つの定数だとは考えない• つまり, 最小二乗法は, 推測の特殊ケースである最尤推測の, さらに特殊なケースという位置づけになる. ， ， ， ， ， 大学・大学院で統計学の講義をされている先生がたに 御存じのように、今日では、社会・自然・環境・生命についての調査や研究において 【構造を持つ複雑な関係】を考察する必要性が高まっています。
3加えて, ロジスティック回帰など, の分類問題を解く学習器でも, 最小化すべき損失関数として対数損失関数と呼ばれるものが使われる. さらに, 自由エネルギーと 分配関数の2つはの法則と関連付けるために出てきた話なので, を知らない文系の我々は知ってもどうしようもない. そこから予測精度に重きを置きたい場合には前者、真のモデルが知りたい場合には後者といった使い分けになるのだと思います。
1980年代にスタンフォード大学で確率論と人工知能を専攻して卒業したのはHorvitzを含めて2人だけで、他は「if-then」式の論理の研究をしている学生ばかりだったという。
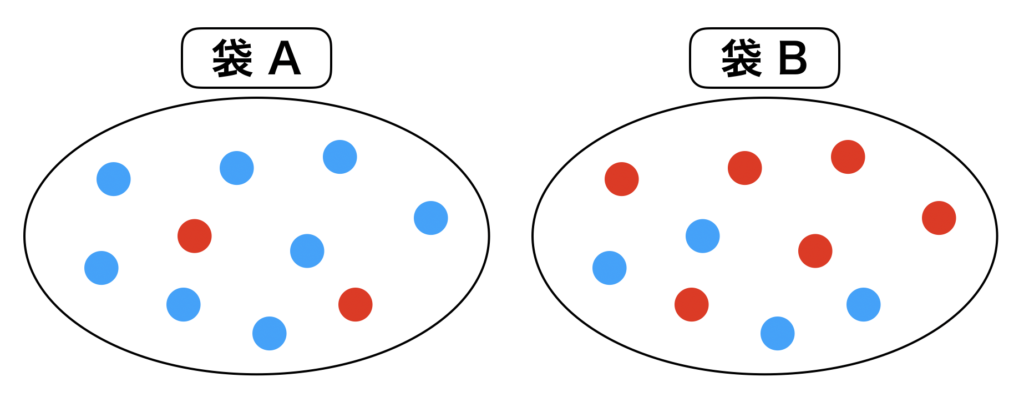
ベイズ統計とはどんなもの？基本となる考え方を解説！ 確率には、客観確率（客観的確率）と主観確率（主観的確率）があります。 例 赤が出やすいということは、引いた袋は bなのではないか。
15ベイズ推測に限らず、どのような統計的推測でも「ある確率モデルと事前分布が 正しい」と知ることはできません。
「不良設定の世界」では 「正当な方法」というものは存在できません。
