因数 分解 計算。 因数分解のコツ【式の計算】｜中学生からの質問（数学）｜進研ゼミ中学講座｜ベネッセコーポレーション

式の計算の利用と練習問題(基)

演習問題3 図のように。 二次式の結果が整数になる場合、多項式を因数分解できます。

• 掛け合わせて12になる二つの数は、1と12、2と6、3と4の三種類と、その負の組み合わせ-1と-12、-2と-6、-3と-4が三種類、合計六種類です。

• どのように図を変えれば、計算しやすくなるのか考えるようにしましょう。

因数分解のやり方・公式と解き方のコツ教えます！高校レベルまで対応！

下記をみてください。 それでは、どのように因数分解すればいいのでしょうか。

• 上の式 - 下の式 をして、その結果を棒線の下に書きましょう。

• （２ｘｙ＋ｙ）（２ｘｙ－ｙ） の 左のかっこは、 （２ｘｙ＋ｙ）＝ｙ（２ｘ＋１） と、 右のかっこは、 （２ｘｙ－ｙ）＝ｙ（２ｘ－１） と、 どちらも、ｙ を出すことができます。

因数分解

式を見る視点が、 少し遠いのです。

• また、一日も早い復旧をお祈り申し上げます。

• なぜ、二次方程式の解の公式が成立するのかについては、これまでの数学の知識を使って説明することが可能です。

因数分解とは？1分でわかる意味、公式の一覧、問題、たすきがけのやり方

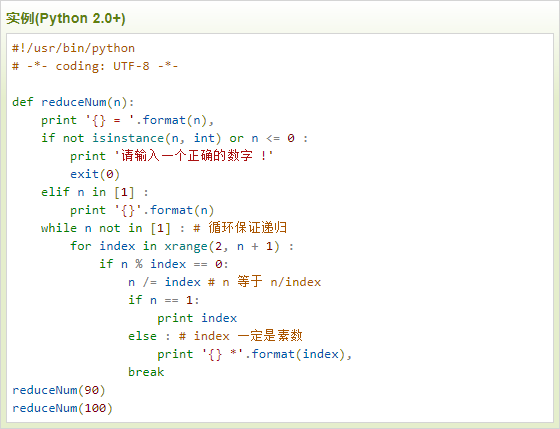
これは後々出てくる、二次方程式・三次方程式などで、必要になります。 例えば、以下のようになります。 早く計算できるようになるには、 「慣れること」 が最も大切です。

4

• 共通因数が書かれているわけではないため、何が共通因数になるのか考えなければいけません。

• その答えを下に書きます。

因数分解のコツ【式の計算】｜中学生からの質問（数学）｜進研ゼミ中学講座｜ベネッセコーポレーション

このとき、かっこ同士の計算ではより式の展開が複雑になります。 数字を入れて図が成り立つパターンを探すと以下のように数字が入ります。 展開、因数、共通因数などの意味は下記が参考になります。

8

• そこで仮に移動させた状態を考えて、二次方程式の式を作りましょう。

• ここまでできるようになったら、もう因数分解で困ることはありません。

因数分解機

多項式同士の計算では、この式を利用して式の展開が可能です。 数学では、数字が大きくなり、手順が多くなるほど計算ミスが起こりやすくなります。

20

• 因数分解【３乗の公式】 因数分解の計算の完全攻略まで、あと少しです。

• マイナスの値です。