角 運動量。 角運動量

角運動量：物理学解体新書

この記事で紹介する 角運動量保存則はある軸に対して回転運動を行っている物体の運動に対して成立する保存則である. したがって、軌道角運動量の場合も含めて、角運動の大きさとその1成分の値は となる。 力矩、 ねじりモーメントとも言う。 加えるが大きいほど、角運動量の変化は大きい。

16

• 角運動量 ＞ ＞＞角運動量とは 角運動量 角運動量とは 並進運動でのに対応するのが、 角運動量だ。

• 上図から分かるように トルク と角運動量は定義が似ている。

角運動量と角運動量保存の法則

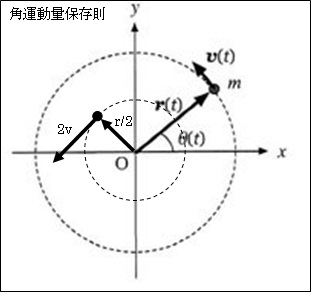
角運動量保存の法則 角運動量が保存されているということは、ベクトルの方向 軸の方向 も一定ということだ。 角速度ベクトルによる表現 ここで角速度ベクトルという物理量を定義します。 力の単位はN（）だが、トルクの単位はN・m（）である。

4

• 角運動量の定義とその変化 角運動量は回転の勢いを表す量ですが，回転運動はどこを中心に回転してるかの基準（回転軸）が必要です。

• の大きな物体の回転を急停止するには、大きなが必要である。

角運動量演算子

概要 [ ] トルクは、との（）で表される量（）である。

• 式の解釈 が小さくても、が速ければが大きい。

• 2 角運動量の大きさといずれか一つの成分のみその値を同時に決めることができる。

角運動量とは

量子的な運動における軌道角運動量のとる値は、マクロな運動（古典力学的運動）の場合と、次の3点で著しく異なっている。

11

• これに応じて，慣性モーメントも回転軸によって値が異なります。

• それと全く同じ大きさを持ち，向きを加えたものを新たに角速度ベクトルとして定義します。

角運動量

電子や陽子、中性子あるいは光子などの素粒子は自分自身の角運動量を有している。 角運動量 回転の勢いを表す量を 角運動量ベクトルまたは単に 角運動量という. 例えば、手を広げた状態でスピンをしていたフィギュアスケート選手が、腕を胸に抱え込んだ姿勢を取ると、回転速度が高まります。 2個あるいはこれ以上の角運動量の和を合成角運動量という。

17

• このことを、並進運動と対比してみよう。

• 全角運動量と L g の差は、質量中心からみたの角運動量とみなすことができる。

角運動量保存則

角運動量と慣性モーメント を、回転半径とので表現した。 運動の勢いの程度がであるように、 角運動量は回転運動の勢いとみなしていいだろう。 角運動量を時間で微分すると、になった。

12

• ただし, 位置 ベクトル と力 ベクトル の内積 スカラー であるエネルギーと 外積 ベクトル であるモーメントという違いがあるので, 和差計算などはできないので注意してほしい. この場合、量子的状態は lと mとで表すことができる。

• これを用いて，角運動量ベクトルを表記してみましょう。