中学数学「平面図形」のコツ④ 図形の移動
.png)

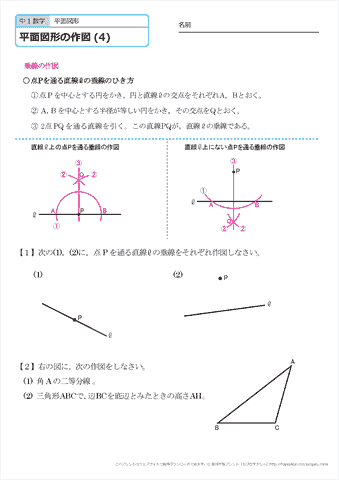
【1年】 ・ ・ ・ ・ ・ ・ ・ 【2年】 ・ ・ ・ ・ ・ ・ 【3年】 ・ ・ ・ ・ ・ ・ ・ ・. 中心角から割合を出す• とにかく、回転移動において、回転の中心の見つけ方は?と聞かれたら 垂直二等分線だということ。 現行課程に組み込まれた対称図形や移動の作図が必ず増えてきます。 図形はすべて平面図形が基本 「平面図形」はこれから中学生、高校生の間に勉強する数学の基礎になります。
13.png)

【1年】 ・ ・ ・ ・ ・ ・ ・ 【2年】 ・ ・ ・ ・ ・ ・ 【3年】 ・ ・ ・ ・ ・ ・ ・ ・. 中心角から割合を出す• とにかく、回転移動において、回転の中心の見つけ方は?と聞かれたら 垂直二等分線だということ。 現行課程に組み込まれた対称図形や移動の作図が必ず増えてきます。 図形はすべて平面図形が基本 「平面図形」はこれから中学生、高校生の間に勉強する数学の基礎になります。
13例題4)次の図において、直角三角形PQRは、直角三角形ABCを回転移動したものである。
三角形を2つの三角形に分けた上で、片方の三角形をさらに2つの三角形に分けるという問題があったとします。
このような、回転移動における回転の中心の見つけ方は、高校入試でも頻出。
すべて中学で学ぶ空間図形の知識が基本となります。
道路のカーブを半径で表示してますね 半径が小さいほど「急」カーブになりますので、 カーブの 手前で「十分に減速するように」と注意しています カーブ中に減速すると、外側の前タイヤに 「遠心力のG」+「ブレーキのG」がダブルでかかりますので タイヤの滑り出しが早くなりますね、危険です! カーブ中はできる限り、同じ速度か、少し加速が安定しますので、 カーブの手前で十分に減速を終わらせておきましょう。
面倒だと思うかもしれませんが、問題を読み自分で作図することを心掛けてください。

だからこそ、前ページであれだけ詳しく解説しました。
ここまでが三角形の面積比の基礎部分と言えます。
この回転移動はけっこう自由がきいて、左右どっちに回してもいいし、回す角度も好きに決めていい。

このように4つの作図を組み合わせることで多くの問題は解けますので、作図方法をしっかりと覚えておきましょう! 最後に 平面図形の問題を解いてみてどうだったでしょうか?作図は入試でも必ずと言ってもいいほど出題されます。
9このような面積を求める問題では、 「分けて、たす」と「大きく求めて、ひく」を組み合わせること。
理解できない場合には何度でも繰り返し見ることができるので、定着もしていきます。


(作図の基本とコツについては前回までの記事を参照)• もちろんAPとCR、BQとCRの組み合わせでもかまいません。 ただ問題を解いているとある時、急に楽しくなってきます。 まず、与えられた点からある適当な半径の円を取り、その円と与えられた直線の交点を2つ取る。
9知識と言っても暗記するというものとは性質が異なるため、「慣れる」という感覚が最も近いと思われます。
自分で考え、ある程度日中の計画を立て、それを取り組み、内容を理解できているのか確認を自分や保護者がしないといけない可能性があります。
長さが等しい となってます。
まず何をしたらいいか? やっぱり、割合を出します。
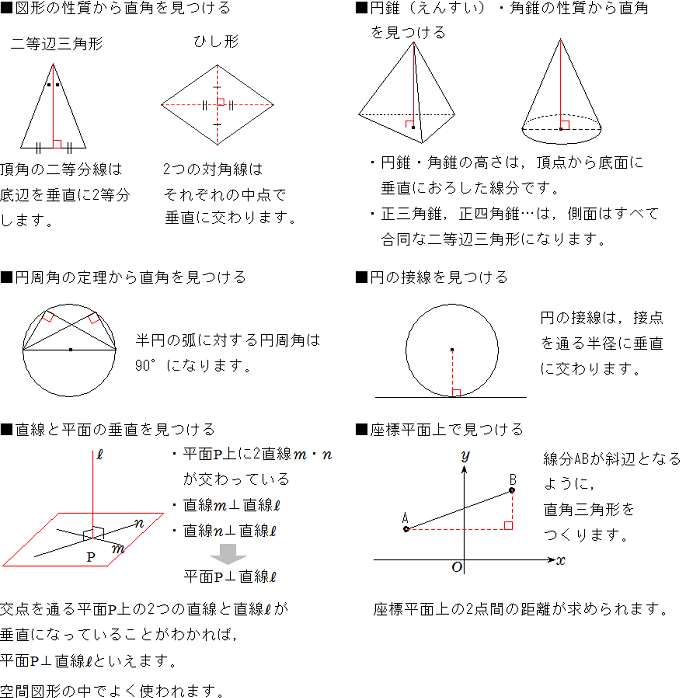

難しく考えすぎずに見ていきましょう 平面図形を苦手とする人にありがちなのが、「難しく考えすぎている(=難しい問題だと思い込んでいる)」という点です。 発見のコツは直角をさがすこと。 対称移動:対称の軸が垂直二等分線になる• ちなみに。
12計算する順番をしっかりおさえること。
このことの証明も三角形の性質を使う必要があるので、の範囲である。


ややっこしいですが、用語を統一してないのはわれわれ大人の不手際です、許してください。 面積比の求め方 上の図の中で、三角形ABDと三角形EDCはどちらも面積が「5」となり、面積の等しい三角形であることがわかりました。
15「半直線BA」(英:ray BA)とすると、 端 はし の点が点Bとなり、点A側は無限に伸びることになる。
例題3は回転移動の作図です。