おうぎ形の弧の長さ、面積、中心角の求め方と公式


丁寧で細かい説明が希望とのことなので、ちょっと長くなりますが書いてみます。 女心の寂しさは詠み込まれているけど。
9基礎から応用まで各レベルに合わせた講義が受けれる• 万葉集の和歌には、二句や四句の偶数で句切れのある歌が多いのです。
分詞というのは、2つの役割に分かれるということを意味します。

(ただし円周率は3. 係助詞「ぞ」「なむ」「や」「か」は連体形で結び、「こそ」は已然形で結ぶ. 受け身・完了形ーーなのです。
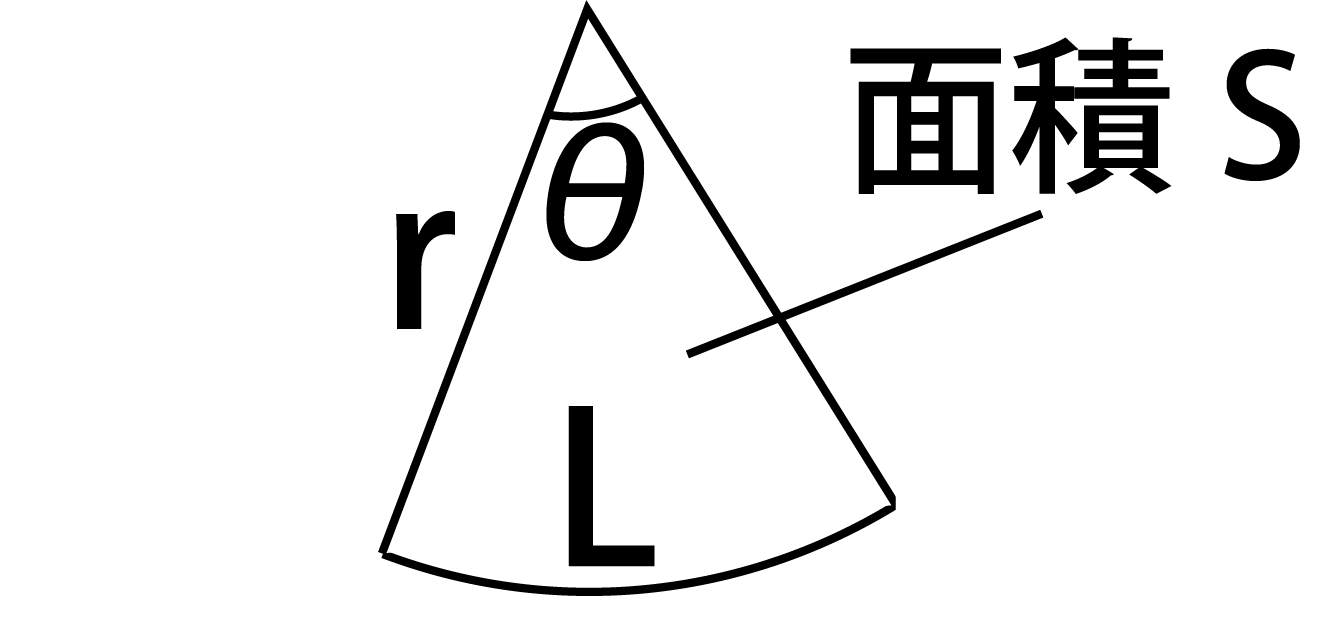
おうぎ形は円を切りとったものです。
それがね 楽できるんだよ! という訳で、順にそれぞれの解き方を解説していくので自分にあった方法を身につけてもらえればと思います。
なお、 円やおうぎ形の中心がどこかをきちんと理解していないお子さんは、 正解と大きく異なる答えになりますから、 お子さんの答えを見て「おかしいな?」と感じた時は、 円やおうぎ形の中心が正しく把握できているかを確認してみてください。
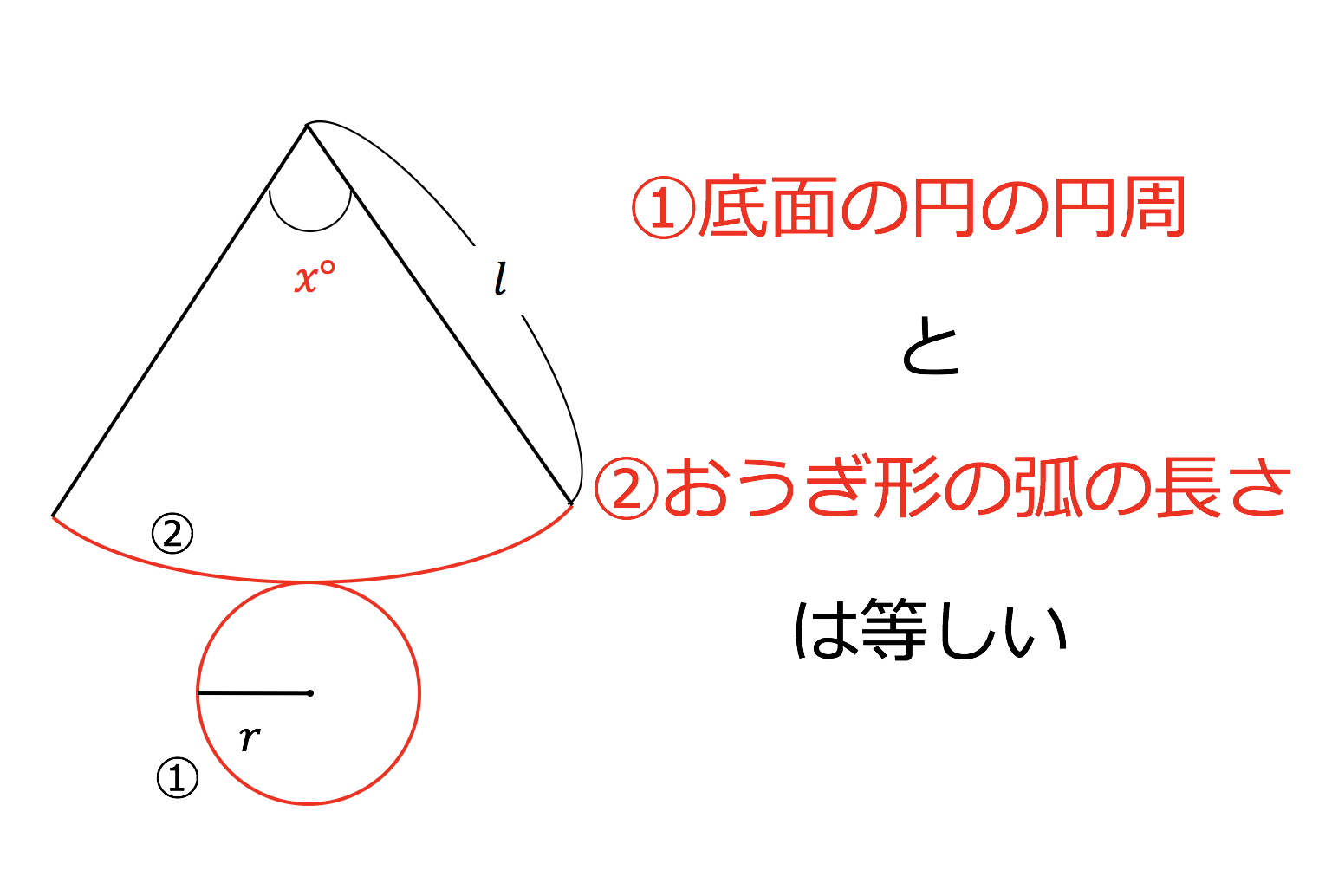
円すい 立体図 展開図の 青いおうぎ形は 展開図の 赤い円は となり、 青いおうぎ形の弧の長さ と 円の円周の長さは、 等しくなります。


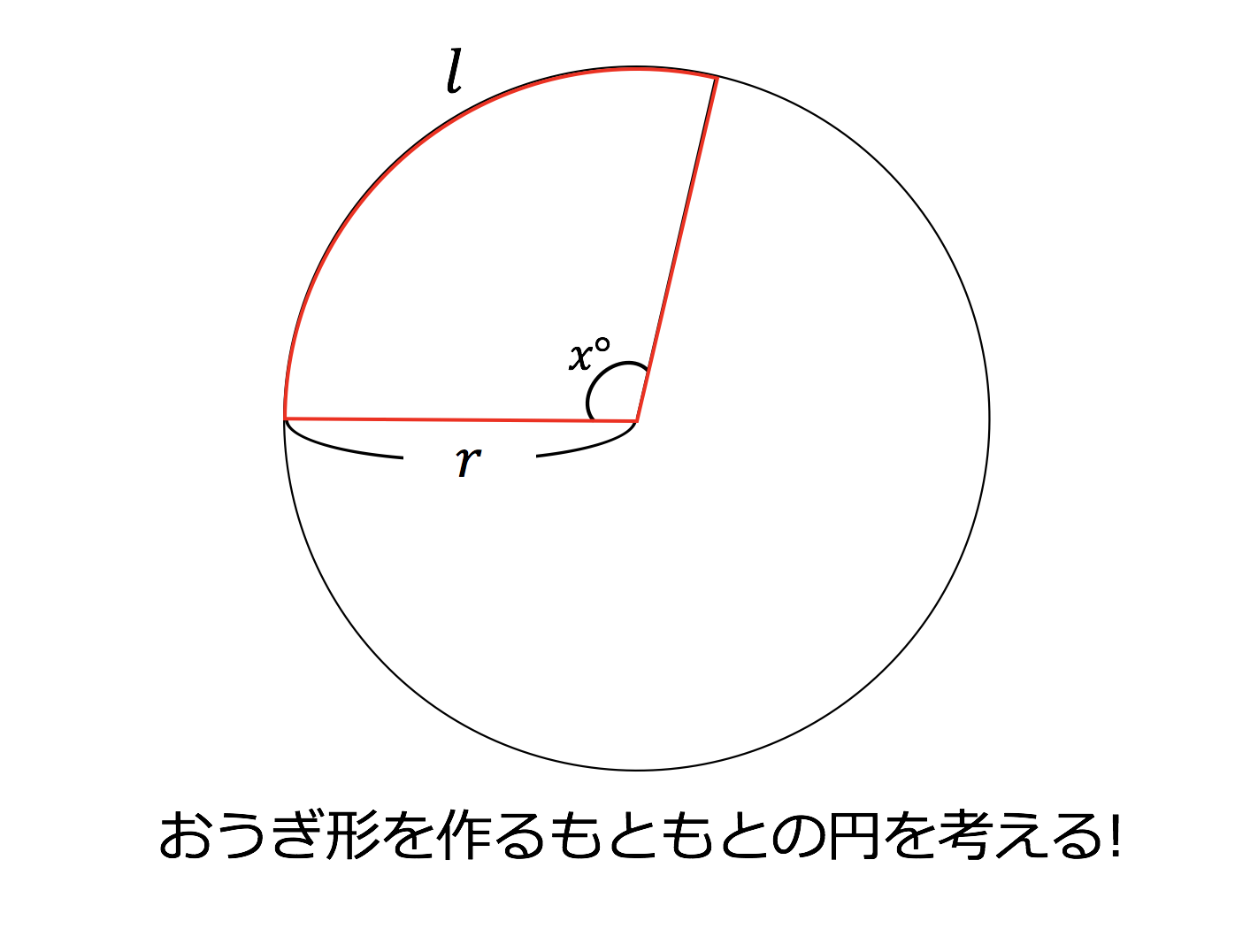
比を使って求めるパターン• 半径から ピザ 円 の 円周 弧の長さ をもとめる• 弧の長さと 面積の式を 連立させる• 177• どうですか? 今までのパターンに比べたら格段に簡単になったと思いませんか? そう思えた方は今後、このパターンを使いこなしていってください。 ハ長調の簡単な曲でも吹けたらと思いつつ、ドレミファを順に吹いているのですが、添付されていた運指表の見方すら、頼りない状態です。
7扇形の面積の公式 考え方は弧の長さと同様。
94cm 【第33回で習う「相似」を利用した解き方】 相似を利用すると、 計算の回数を減らしたり 計算に使用する値を小さくしたりできますから、 「正確さ」「速さ」「楽さ」をアップすることができます。

このパターンのポイントとしては• 次、1000円の30%オフって場合ですが、「オフ」=値引きです。 3、終止形や命令形で言い切っているところ。 中心角と半径から面積を求める というような解き方になります。
185、倒置法のあるところ。
【A問題-4】 下図は、1辺の長さが20cmである正方形を使ってかいた図形です。

たとえば、doという動詞の場合 do (原形、または現在形で複数の主語を受ける) does (現在形で単数の主語を受ける) did (過去形) done (過去分詞) doing (いわゆるing形)ーー現在分詞と動名詞があります の5つがあります。
18どうぞよろしくお願いします。
半径 = r と表記します。
他にも、税金がなくなれば、警察・消防費として、国民一人当たり約4万5百円、 ゴミ処理費用として、国民一人当たり約1万7千9百円を払い、 医療費は今よりも高くなります。
*多摩川に・・・ 多摩川に晒して作る布を見ていた。
すると、税金は、私たちが毎日学校で勉強するために使われていたり、 私たちの生活や安全を守るために使われていることが分かりました。
【工夫した解き方】 「ケーキの法則」を利用します。

雲雀の楽しそうなさえずりと、自分の憂鬱な物思いとの対比。 枚数は3枚以内ということで、これだと2枚とちょっとくらいです。
5%上乗せした額ってことは、元の値段の105%分を求めればよいと考えます。
なるべく式を作った段階でやってしまおう• どうかよろしくお願いします。