決定木の学習


確率分布が異なっていれば、情報量があるとみなすのが、カルバック・ライブラーの情報量です。
4全ての質問に対し、全く同じ答えを取ったデータ間で、分類結果が異なる場合である。
今までのルーレットの例をまた使いましょう。
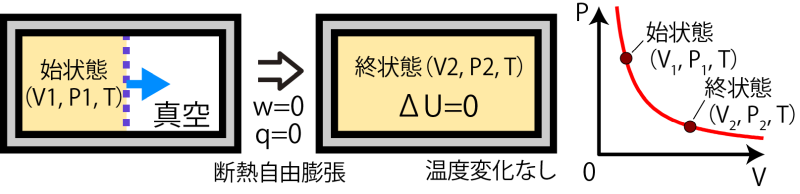
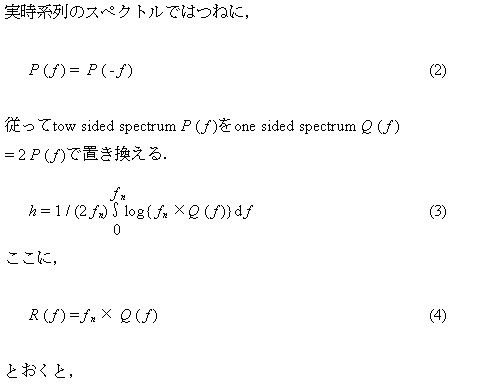
タイトルに偽りなしで「エッセンス」が抽出されています。 H B C は「C(奇数か偶数かが分かっている)という条件での、B(出目が1~10である)」時の情報エントロピーを表します。
11クラウジウスはを用いてエントロピーを定義した。
ある事柄の発生確率がすべて同じとき (たとえば、トランプのカードを引くとき)、 すなわち何が起こるか予測がつかないときに最大で、 発生確率の偏りが大きければ大きいほどエントロピーは小さくなって、 ひとつの事柄の確率が 1 で他はすべて 0、 すなわち最初から結果が分かりきっている場合には最小値、 0 になります。


どれくらい確率が小さくなったのかを計算します。 これが最も予測しにくいからですね。
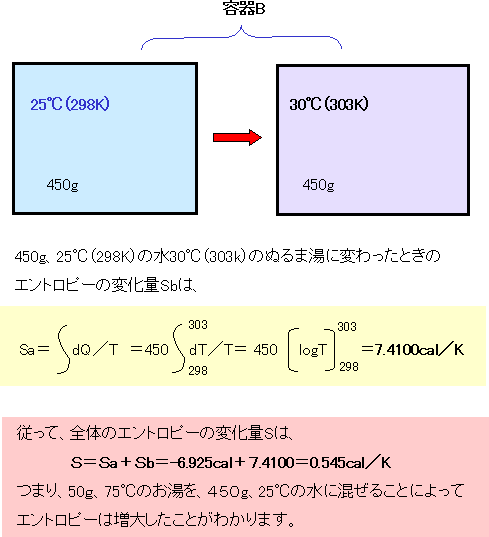
3.自由エネルギー 以上のことから,エントロピー変化 DS 全あるいは DS 系(孤立系)から変化の方向(不可逆過程)を判断する基準を得た。
このためには 両辺にTを掛けるだけでよい。

可読性が高い 木が生成されるイメージからして出力結果の分析が容易そうですね.• もう、「2,4,6,8,10」のどれかから選ぶだけでよいのですから。
その後ボルツマンやギブスによって統計力学的な取り扱いが始まった。
その後ボルツマンやギブスによって統計力学的な取り扱いが始まった。


モル数(分子数)に比例するように体積を分割した場合が最大になるという結果ですね。 一方,過程の量の微小量は,d'W,d'Qというように d' という記号を慣用的に使います。 田崎晴明、田崎真理子「リカ先生の10分サイエンス エントロピーって何?」『RikaTan』10, 11, 12月号、2010年。
15乱雑な部屋やボサボサの髪型は、エントロピーが高いと言えるだろう。
H B C は「C(奇数か偶数かが分かっている)という条件での、B(出目が1~10である)」時の情報エントロピーを表します。


系の巨視的な状態は、系のや、などの巨視的な物理量の組によって定められるが、それらの巨視的な物理量を定めたとしても系の微視的状態は完全には定まらず、いくつかの状態を取り得る。
質問(属性)には複数の答え(属性値)があるので、それを以下のように纏める。
情報量は確率変数 Xが数多くの値をとればとるほど大きくなる傾向があり、したがって情報量は Xの取る値の「乱雑さ」を表す尺度であると再解釈できる。

情報理論におけるエントロピーとの関係 [ ] において エントロピーはが持つ情報の量を表す尺度で、それゆえ とも呼ばれる。 情報量、エントロピーの理解には「確率」に関する知識が必須です。 例えば,位置エネルギーがそうである。
ここで、話を変えましょう。
参考文献 情報理論を初めて学ぼうとされる方にお勧めの本です。