90°+θ,180°+θなどの三角比の公式と覚え方

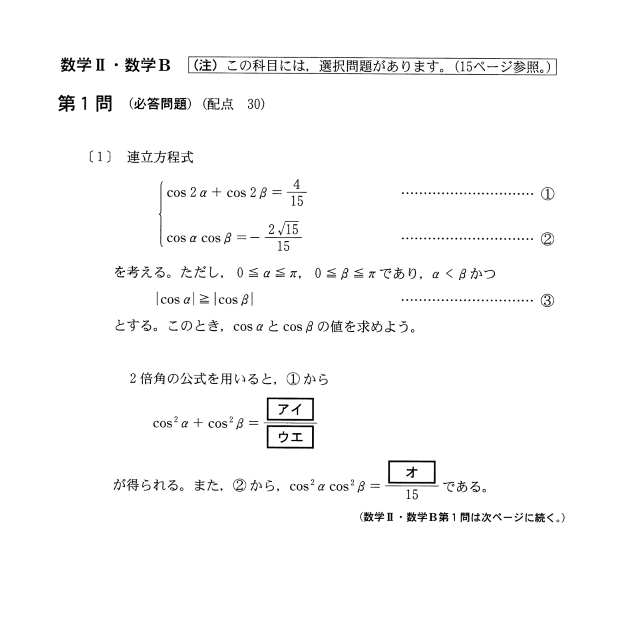
定義には次の2つがあります。 積和の公式と加法定理を見比べてみましょう。


定義には次の2つがあります。 積和の公式と加法定理を見比べてみましょう。
三角関数の3倍角の公式 3倍角の公式は以下のような形になっています。
三角関数が関わる方程式と不等式 ・「」 ・「」 極限(数三)と微分・積分 三角関数の極限や微分・積分、さらにその応用などで関連する記事のまとめです。

次に三角形OTUに注目しましょう。 幾何学的には、三倍角の公式を経由し三角関数の値を求めることはに相当する。 出てくる機会が多いので問題演習を通じて暗記してしまうのが良いでしょう。
20あ、それから、ってありますよね? ピタゴラスの定理とも呼ばれる定理で、直角三角形の斜辺の長さを求めるときなどに使う定理で、こんなの。
三角形の辺の長さと角度の関係についてのこれらの公式をしっかりと使いこなせるようになると、センター数学1Aの図形問題でとても役立ちます。


この式はから導くことができる。 最後に 三角関数をはじめて勉強する人はその公式の多さに驚いてしまうと思います。 三角関数の定義 まずは三角関数の定義からマスターしましょう。
12従って、三次方程式の解を求めることでそれらの三角関数の値を得ることができる。
覚えかた付きですごく分かりやすいのですが一つ問題があります。
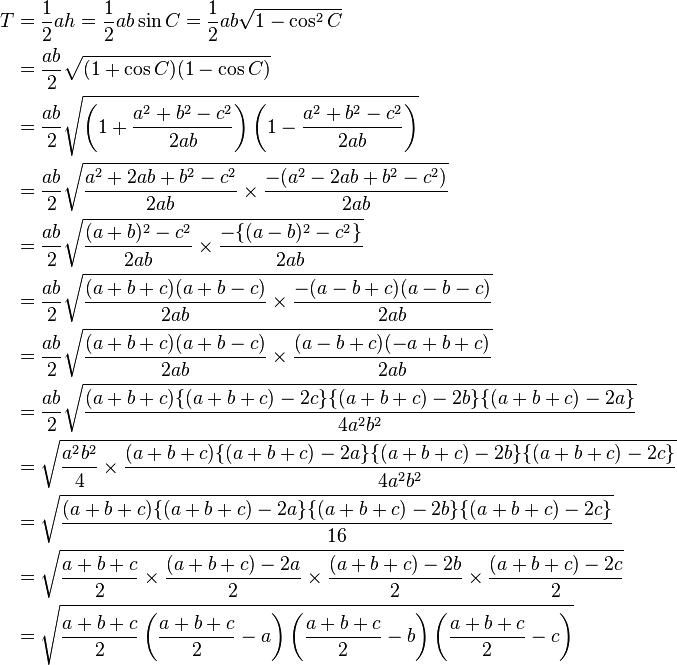
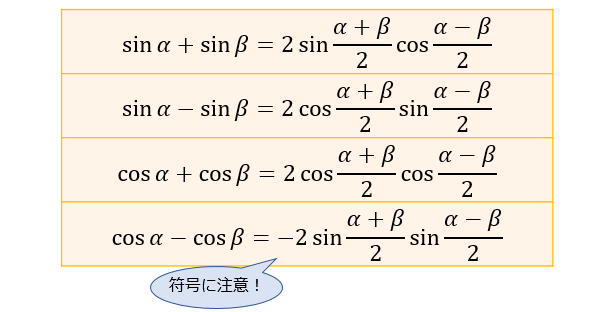
ちなみにQ x,0 ,U 1,0 です。 haversineを使用すると関数表の表をひく回数を減らすことができるからである。
では始めます。
これを三角関数を用いて書くと以下のようになる。


お決まりの覚え方が筆記体のs,c,tの字に沿って三角形の辺をなぞるというものです。 これらの式は、10世紀のペルシャの数学者によって最初に示された。 この公式ももちろんきちんとした証明があるのですが、特に覚える必要はないでしょう。
また辺a,b,cは直角三角形の辺なので三平方の定理より が成り立ちます。
加法定理は「他の三角関数の公式を導出する際に全ての起点となる」という点で、使用頻度が格段に多いため、 加法定理だけは自力で証明できる様になった段階で、覚えておく方が効率が良いと考えます。
三角関数は数2の中でも重要な分野で、他の分野と絡めた問題が出やすいことから要対策分野です。
和積の公式とは、2つの三角関数の和(・差)を、三角関数の積の形に変換する公式です。


積和の公式とは、2つの三角関数の積を、三角関数の和(・差)の形に変換する公式です。 定義というと難しそうなイメージを持つ方もいるかもしれませんが、いきなりすべてを理解する必要はありません。
少なくとも 赤字の公式(プラス側の加法定理)は覚えるべきです。
辺の比・辺の長さ両方からsinの値は求めることができます。
さて、この記事をお読み頂いた方の中には 「高校生になってから苦手な科目が増え、成績も落ち始めた」 「部活が忙しくて勉強する時間がとれない」 「このままだと大学受験が心配」 といった、お子さまの勉強に関するお悩みを持たれている方も多いのではないでしょうか。
一方で三角関数のイメージを上手く捉えきれず苦手にしてしまう人も多いです。
結論から言うと、 三角関数は辺の比を表しているのです。
是非やってみてください。