余弦定理正弦定理。余弦定理

正弦定理と余弦定理

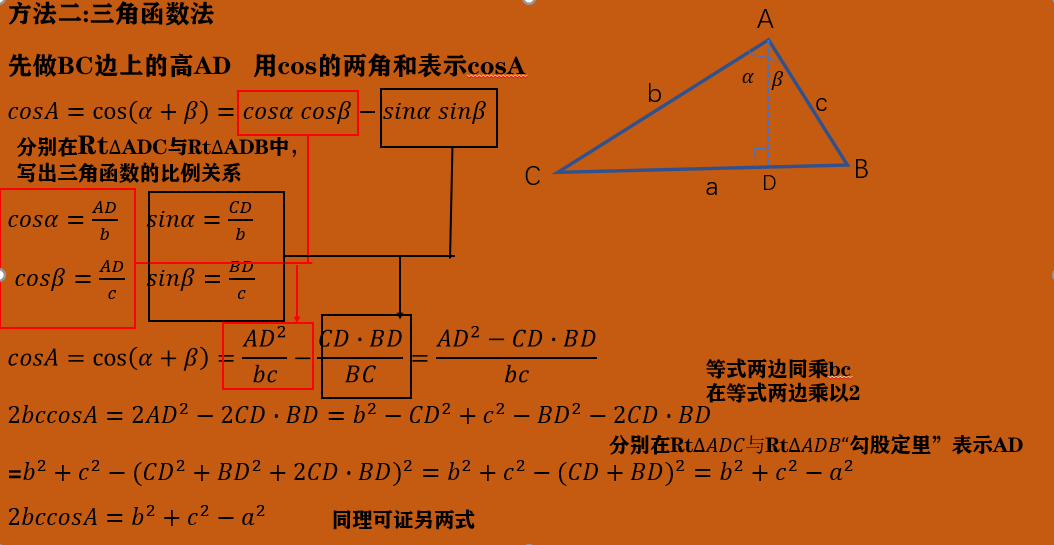
そこで、これら2つの定理の使い分けの仕方を紹介します。

大学名は、2019年度入試時点のものです。
もともと三角比は古代ギリシャのプトレマイオスの角に対する弦の長さの研究を起源とするようだが、それは現在のような三角比の概念ではなく、天文学の研究のために必要な数表としての扱いであったようだ。

正弦定理の証明

「三角比の問題」と気がついたら問題を解き始める前に公式を書き出しておいて、大問の序盤でちょっとでも悩んだら「使っていない定理はないか？」と確認してみると良いことあります。

三角比の方程式の解き方を思い出しましょう。
いくつか問題を解いていきましょう。

正弦定理と余弦定理の公式の証明

私が、これらの定理を学校教育で学んだのは、高校２年生のときである。語呂合わせで覚える方法• 使うときには全く意識しないですが、覚えておいて損はないと思います。まず、三角形ABCですが、３辺が与えられているので、三角形の大きさ・形がただ１通りに決まります。

web講義・問題、ハンドブック、添削7回分。
図6 図6において、頂点 Cから辺 ABに引いた垂線を CHとする。

正弦定理の解説と証明

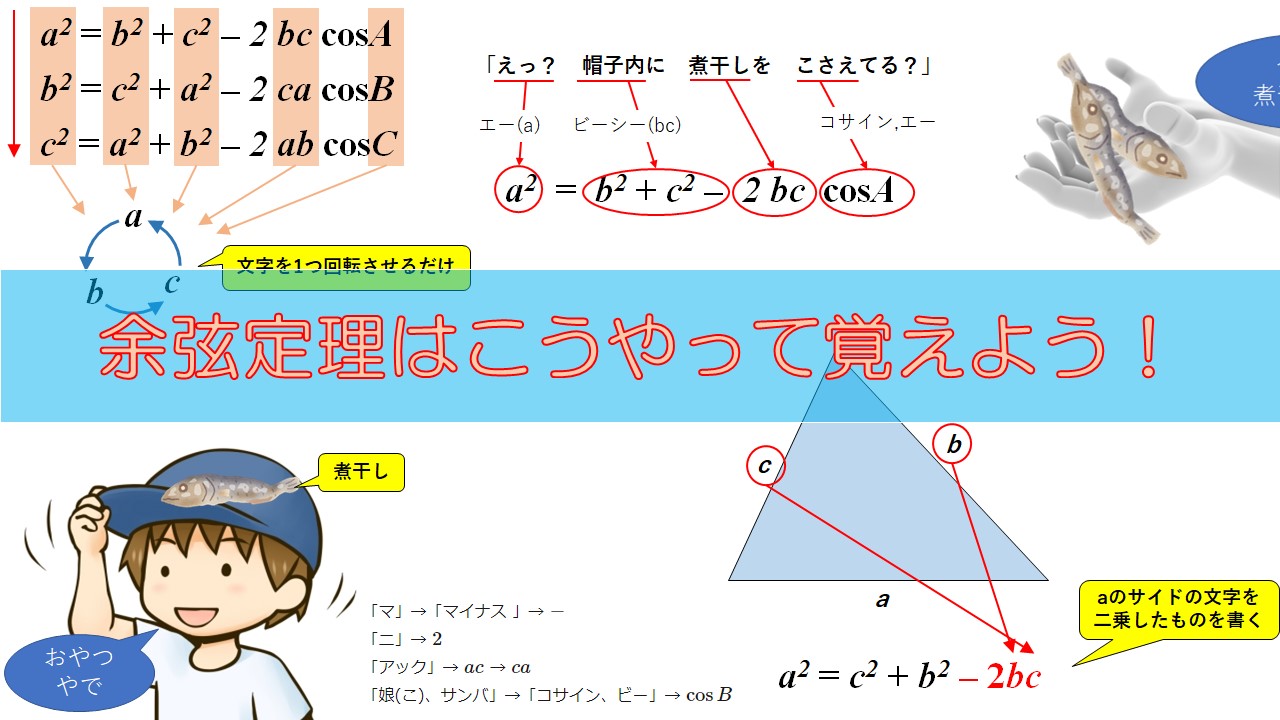
また、余弦定理は、三平方の定理の応用として証明される。余弦定理を語呂合わせに頼らず覚えたい余弦定理の覚え方を紹介します。解説していきましょう。

ストーリーはこんな感じらしいです。
つまり、三角形の辺の長さ・角の大きさがただ１通り決まる条件を満たしているため、三角形ABDの辺の長さ・角の大きさもただ１通りに決まるはずです。

正弦定理とは？公式や余弦定理との使い分けをわかりやすく解説！

$定理正弦余弦定理$ 定理正弦余弦定理

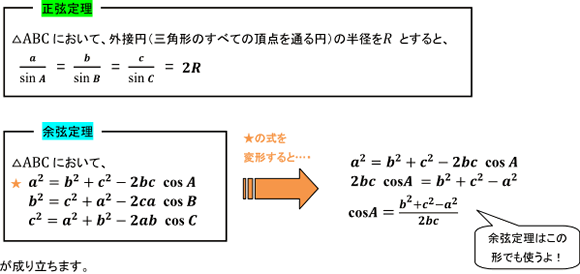
【数学IA】正弦定理と余弦定理の利用大学入試数学の考え方と解法 MathJax. この３つの等式の両辺に、それぞれ、ａ、－ｂ、－ｃを掛けて、辺々加えれば、を得ることができる。（平成２２年９月２５日付け）、が成り立つとき、が成り立つことを示す。余裕のある人は、公式の変形バージョンも覚えておくと、スピードアップして解くことができますよ！. まとめ正弦定理・余弦定理の内容とそれらを用いた代表的な問題の解き方を説明しました。