【フーリエ変換とは?第二編】複素形式のフーリエ級数とは何?その導出方法についてご紹介 │ アドオン. ねっと

にはが用いられる。

にはが用いられる。
2ウェーブファイルを操作するプログラムの一部を、改造させていただきました。
なので、 奇関数の初項 は計算する必要がないのです! 2 f t が偶関数・奇関数の場合 周期関数 が偶関数・奇関数の場合はより少ない計算量でフーリエ級数展開を求めることができます。
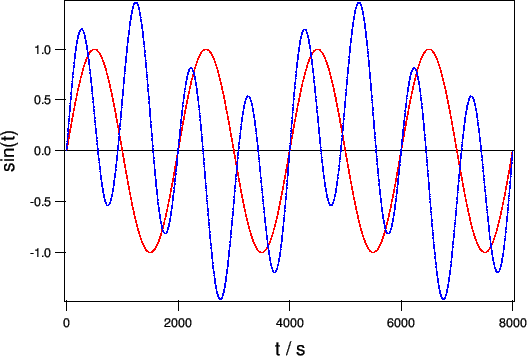
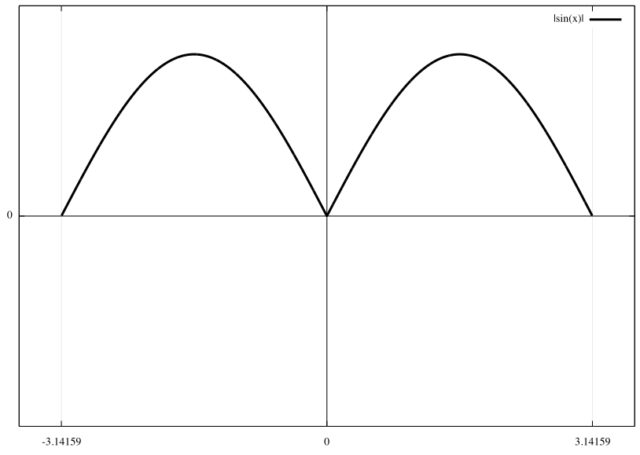
フーリエの研究の前までには、一般的な形での熱伝導方程式の解法は知られておらず、熱源が単純な形である場合、例えばなどの場合の特別な解しかえられていなかった。
3オイラーの公式 上記をちゃんと計算をするためには, オイラーの公式が必要です. は, を含んでいるので、あらたに と名づけましょう。
これは「f x が微分可能」 という意味になります。
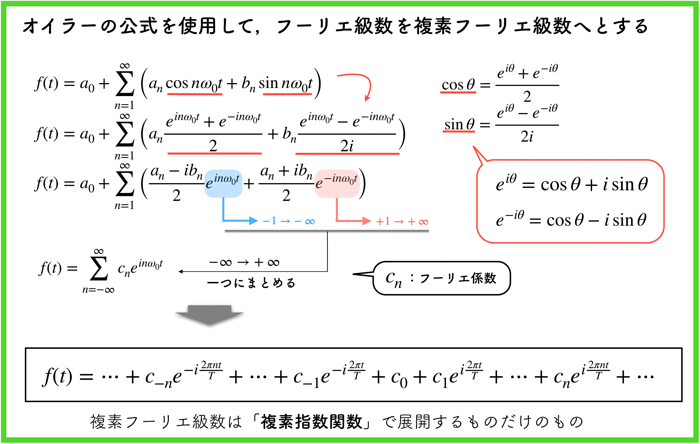

色をつけて公式を少しわかりやすくしてみました! つまり、周期関数 を 偶関数 , , , …… と奇関数 , , , …… を用いて表せるよってことなのです! 少し難しい用語を使うと、周期関数 を偶関数 , , , …… と奇関数 , , , …… の 1次結合で表せるってことです! しかし、フーリエ係数 , の求め方が複雑だったりなぜか初期値が となってたり がなかったりしますね。 まとめ 積分の中身は複素数ですが, 虚部が消えてちゃんと綺麗になりました. わかりやすくするために 7 式の和の部分を展開します。 余裕があれば複素フーリエ級数展開、フーリエ変換についてもまとめてみようかと思います。
17ii cos の項の導出 つぎに偶関数 のフーリエ係数 を導出してみましょう。
今回証明したのは「ディリクレの収束定理」というやつで,電気信号を扱う上ではこれで十分かと思います。
ここまで来ても,区分的なめらかな関数だったら sin 関数と cos 関数だけで表現できてしまうなんて,不思議です。 増分に-を付けてみると ところでBnは 2-7 なので つまり、 2-8 で波が表されることが分かります。 符号違いの同値が交互に出てくるので次のようにまとめることが出来ます. 」と思った人もいるかもしれません。
142-4 2-5 足し算 引き算をしあらたに と名前をつけます。
単位インパルスと、インパルス列を比べてみました。
筆者もその一人ですが、言葉の概念だけを知っていて分かったつもりになっていますが、その詳細については理解していない所が多い為、今回は筆者の備忘録がてらフーリエ変換についてまとめていきたいと思います。
こんにちは、ももやまです。
どうやってもっと綺麗にするのか, という答えが複素形式のフーリエ級数展開です. 適切な窓、時間分解能があれば、単一スペクトルのはずや。
係数 を計算してみましょう。
普通のフーリエ級数展開(復習) 複素形式のフーリエ級数展開をやる前に, 普通のフーリエ級数展開を復習しておきたいと思います. このことからfの 複素フーリエ級数は下記のようになります。 STEP 3. この(1)がフーリエ級数展開 と呼ばれています。 。
20を使ってまとめておく。
工学部の数学で、「フーリエ級数展開」という言葉を聞いたことがある人は多いかと思います。